Shear Strain Formula: A Practical Guide Explained

The principles of material deformation are crucial in civil engineering, influencing structural integrity assessments. Shear strain, a dimensionless quantity, represents the angular distortion of an object under tangential stress. The American Society for Testing and Materials (ASTM) provides standardized methods for experimentally determining shear strain. A practical understanding of the shear strain formula allows engineers to accurately predict material behavior, aiding in the design of safer and more reliable structures.

Image taken from the YouTube channel Infinity Learn NEET , from the video titled Shear Stress and Shear Strain | Mechanical Properties of Solids | Don't Memorise .

Shear strain is a fundamental concept in understanding how materials behave under stress. It specifically quantifies the deformation resulting from tangential, or shear, forces.

This introduction will lay the groundwork for understanding the relationship between shear stress and shear strain. Furthermore, we'll explore its practical significance across diverse engineering disciplines.

Defining Shear Strain: Quantifying Tangential Deformation

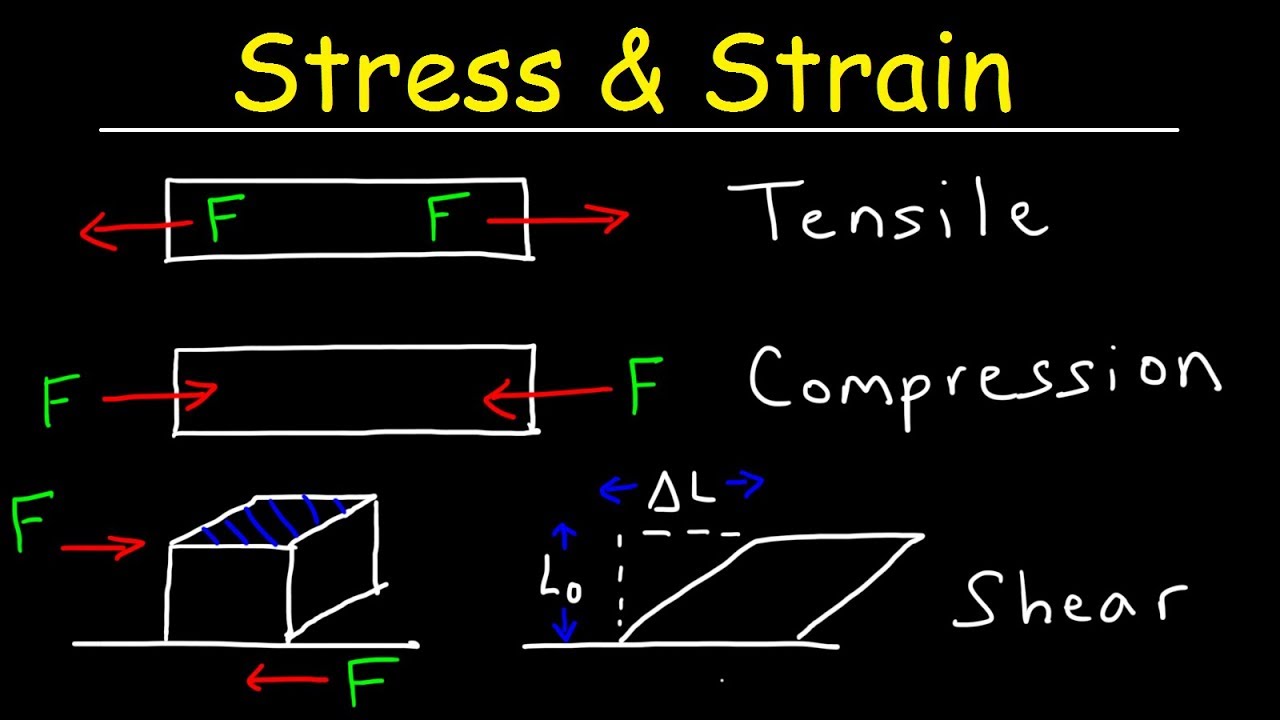
Shear strain, often denoted by the symbol γ (gamma), is defined as the change in angle, measured in radians, between two lines that were initially perpendicular in a material. This change in angle arises when the material is subjected to shear stress.

In simpler terms, it represents the "sliding" or "skewing" of a material's internal planes relative to one another. It's a dimensionless quantity, as it's a ratio of lengths, but is often expressed in units of radians.

The magnitude of shear strain directly reflects the extent of this deformation, providing a precise measure of how a material distorts under tangential loads.

The Relationship Between Shear Stress and Shear Strain

Shear stress (τ) is the force acting tangentially per unit area. When a material is subjected to shear stress, it experiences shear strain.

This relationship is crucial: shear stress causes shear strain. The material's resistance to this deformation is a key property.

Within the elastic limit of a material, shear stress and shear strain are linearly related, as described by Hooke's Law for shear. Beyond this limit, the relationship becomes non-linear.

This linear relationship is critical for many engineering calculations and approximations.

Importance of Shear Strain in Engineering and Material Science

Shear strain analysis is integral to a wide range of engineering applications. It plays a vital role in predicting material behavior and ensuring structural integrity.

In mechanical engineering, understanding shear strain is crucial in the design of shafts, gears, and other machine elements subjected to torsional loads. Proper shear strain analysis helps prevent failures due to excessive deformation or yielding.

Civil engineers rely on shear strain principles to analyze the stability of soil, design foundations, and evaluate the safety of bridges and buildings under various loading conditions. In materials science, shear strain measurements are essential for characterizing material properties and developing new materials with enhanced shear resistance.

Even in geophysics, shear strain data can aid in understanding fault line behavior and potentially predicting seismic events.

Ultimately, shear strain analysis provides a crucial framework for understanding and predicting material behavior under tangential forces, contributing to safer, more reliable engineering designs and a deeper understanding of material properties.

Fundamental Concepts: Defining Shear Deformation

Shear strain is a fundamental concept in understanding how materials behave under stress. It specifically quantifies the deformation resulting from tangential, or shear, forces. This section will lay the groundwork for understanding the relationship between shear stress and shear strain. Furthermore, we'll explore its practical significance across different fields.

Deformation Overview

Deformation, in general, refers to any change in the size or shape of a body. It can be caused by external forces, changes in temperature, or other factors. There are several types of deformation, including tensile, compressive, and shear deformation.

Shear deformation, also known as angular deformation, is unique because it involves a change in the angle between lines initially perpendicular to each other within the material. Imagine a rectangular block being pushed sideways on its top surface while the bottom surface remains fixed. This is a visual representation of shear deformation.

Unlike tensile or compressive deformation, which involves stretching or shortening, shear deformation involves a sliding of one layer of the material over another.

Angle of Twist (γ)

The angle of twist, denoted by the Greek letter gamma (γ), is a crucial parameter in quantifying shear strain. It represents the angular displacement, measured in radians, between two lines that were initially perpendicular within the material before the application of shear stress.

Imagine our rectangular block again. As the top surface is displaced, the vertical sides of the block tilt, creating an angle with respect to their original vertical position. This angle, measured in radians, is the angle of twist.

It is important to remember that the angle of twist directly reflects the magnitude of the shear deformation. A larger angle of twist indicates a greater degree of shear strain. A visual representation of this effect is helpful in understanding the concept.

Hooke's Law (for Shear)

Linear Relationship

Within the elastic limit of a material, shear stress and shear strain exhibit a linear relationship. This relationship is described by Hooke's Law for shear, which states that shear stress is directly proportional to shear strain.

Mathematically, this is expressed as: τ = Gγ, where τ represents shear stress, γ represents shear strain, and G is the modulus of rigidity (also known as the shear modulus), which we will discuss later.

This linear relationship is fundamental to many engineering calculations. It allows us to predict the shear strain in a material if we know the applied shear stress and the material's shear modulus.

Limitations and Applicability

It's crucial to understand that Hooke's Law for shear is only valid within the elastic limit of the material. Beyond this limit, the material's behavior becomes nonlinear, and the relationship between shear stress and shear strain is no longer linear.

Additionally, Hooke's Law assumes that the material is isotropic, meaning its properties are the same in all directions. For anisotropic materials, such as wood or composites, the relationship between shear stress and shear strain is more complex. Furthermore, temperature, rate of loading, and other environmental factors can affect the validity of Hooke's Law.

Modulus of Rigidity (Shear Modulus, G)

Definition and Significance

The modulus of rigidity, often referred to as the shear modulus and denoted by G, is a material property that reflects its resistance to shear deformation. It represents the ratio of shear stress to shear strain within the elastic limit.

In essence, the shear modulus indicates how stiff a material is when subjected to shear forces. A material with a high shear modulus will deform less under a given shear stress compared to a material with a low shear modulus.

The shear modulus is a critical parameter in engineering design, particularly when dealing with components subjected to torsional loads or shear forces.

Factors Affecting Shear Modulus

The shear modulus of a material is influenced by several factors, including:

• Temperature: Generally, the shear modulus decreases as temperature increases. This is because higher temperatures increase atomic vibrations, making it easier for the material to deform.
• Material Composition: The type of atoms and their arrangement within the material significantly affect the shear modulus. Different materials will have vastly different shear moduli.
• Microstructure: The microstructure of the material, including grain size and the presence of defects, can also influence the shear modulus.

Linear Approximation

Simplifying Calculations

In many practical engineering applications, the shear strains involved are relatively small. In these cases, we can use a linear approximation to simplify calculations.

This approximation assumes that the angle of twist (γ) is small enough that sin(γ) ≈ γ. This allows us to use the small-angle approximation to simplify trigonometric calculations, making the analysis more manageable.

Conditions for Valid Use

The linear approximation is valid when the shear strain is small, typically less than 0.1 radians. Beyond this limit, the approximation becomes less accurate, and it is necessary to use more precise trigonometric functions.

Care must be taken to ensure that the shear strain is within the acceptable range for the linear approximation to be valid.

Radians

Importance of Radians

In shear strain calculations, it is essential to use radians as the unit for angle measurements. Radians are the standard unit in most scientific and engineering calculations, including those involving trigonometric functions.

Using degrees instead of radians will lead to incorrect results because the mathematical relationships used in shear strain analysis are based on radians. Therefore, always convert angles to radians before performing any shear strain calculations.

Material Behavior Under Shear: Elasticity, Plasticity, and the Stress-Strain Curve

Shear strain is a fundamental concept in understanding how materials behave under stress. It specifically quantifies the deformation resulting from tangential, or shear, forces. This section will lay the groundwork for understanding the relationship between shear stress and shear strain. Furthermore, it will describe how these properties determine the material's response to external stresses.

Materials exhibit diverse behaviors under shear stress, broadly categorized as elastic and plastic. Understanding these behaviors is crucial for predicting material performance in various engineering applications. These properties are graphically represented through the shear stress-strain curve.

Elasticity: The Reversible Response

Elasticity describes a material's ability to return to its original shape and size after the removal of an applied shear stress. Within the elastic region, the deformation is temporary and fully recoverable.

This behavior is characterized by the linear portion of the shear stress-strain curve, where stress and strain are directly proportional. Hooke's Law for shear accurately describes this relationship, defining the material's shear modulus (G), also known as the modulus of rigidity.

Plasticity: Permanent Deformation

Plasticity, conversely, refers to the material's propensity to undergo permanent deformation that remains even after the shear stress is removed. This behavior occurs once the applied stress exceeds the material's elastic limit.

Beyond this point, the material experiences irreversible changes in its internal structure, resulting in a permanent set. The material has yielded and will no longer return to its original shape. This phenomenon is critical to understanding material failure.

The Shear Stress-Strain Curve: A Comprehensive View

The shear stress-strain curve provides a comprehensive graphical representation of a material's behavior under shear loading. It plots shear stress on the y-axis against shear strain on the x-axis, revealing key material properties.

Graphical Representation and Interpretation

The initial linear portion represents the elastic region. As the stress increases, the curve deviates from linearity, marking the onset of plastic deformation. The curve continues to rise until it reaches a peak, representing the material's ultimate shear strength. Beyond this point, the material begins to neck or fracture.

Key Points on the Curve

Elastic Limit

The elastic limit is the maximum stress a material can withstand without permanent deformation. Up to this point, the material will return to its original dimensions upon unloading.

Yield Strength

The yield strength is the stress at which the material begins to exhibit significant plastic deformation. It is often defined as the stress corresponding to a specific amount of permanent strain, such as 0.2% offset.

Ultimate Shear Strength

The ultimate shear strength represents the maximum shear stress the material can withstand before failure. It is the highest point on the shear stress-strain curve. After this point, the material weakens and eventually fractures.

By analyzing the shear stress-strain curve, engineers can determine critical material properties. These properties are important for designing safe and reliable structures and components. The concepts of elasticity and plasticity, as revealed by the curve, are indispensable in material selection and structural integrity assessments.

Applications in Engineering: Real-World Examples of Shear Strain Analysis

Shear strain is a fundamental concept in understanding how materials behave under stress. It specifically quantifies the deformation resulting from tangential, or shear, forces. This section will explore the diverse applications of shear strain analysis across various engineering fields, providing concrete examples of how these principles are utilized in real-world scenarios.

Mechanical Engineering: Optimizing Designs and Mitigating Risks

In mechanical engineering, understanding shear strain is crucial for designing robust and reliable machine components. Shear strain analysis plays a critical role in optimizing designs, preventing failures, and ensuring the longevity of mechanical systems.

Design of Machine Elements

Many machine elements, such as shafts and gears, are subjected to torsional loads that induce shear stresses and strains. Shear strain analysis helps engineers to accurately predict the deformation and stress distribution within these components.

This analysis ensures that the designs can withstand the applied loads without exceeding the material's yield strength or experiencing excessive deformation. For example, when designing a drive shaft, engineers use shear strain calculations to determine the appropriate diameter and material selection to prevent torsional failure under maximum operating torque.

Analysis of Stress Concentrations

Stress concentrations are localized areas within a component where stress levels are significantly higher than the average stress. These areas are often found near geometric discontinuities, such as holes or sharp corners.

Shear strain analysis is essential for identifying and mitigating these stress concentrations, which can lead to premature failure. By using techniques like finite element analysis (FEA), engineers can visualize the distribution of shear strain around these discontinuities.

This allows them to optimize the design to reduce peak stress levels and improve the overall fatigue life of the component. Techniques such as introducing fillets or modifying the geometry can effectively redistribute stress and minimize the risk of failure.

Civil Engineering: Ensuring Structural Integrity and Stability

Shear strain analysis is indispensable in civil engineering for ensuring the structural integrity and stability of buildings, bridges, and other infrastructure. Understanding how shear forces affect these structures is vital for preventing catastrophic failures and ensuring public safety.

Structural Analysis of Buildings and Bridges

Buildings and bridges are subjected to various shear forces due to wind loads, seismic activity, and traffic loads. Shear strain analysis is used to evaluate the stability and safety of these structures under these conditions.

Engineers use computational models and analytical techniques to determine the shear stress and strain distribution within structural elements like beams, columns, and connections. This analysis helps to identify potential weak points and ensure that the structure can withstand the applied loads without excessive deformation or failure.

For example, shear strain analysis is critical in the design of bridge supports to ensure they can handle the shear forces induced by heavy traffic and environmental factors.

Soil Mechanics and Stability Analysis

Soil, as a construction material, exhibits shear strength that determines its ability to support loads and maintain stability. In soil mechanics, shear strain analysis is crucial for assessing the stability of soil slopes, foundations, and retaining walls.

Engineers analyze the shear strain characteristics of soil to predict its behavior under different loading conditions. This information is essential for designing stable foundations for buildings and bridges, as well as for preventing landslides and soil erosion.

For example, slope stability analysis involves evaluating the shear strain distribution within a soil slope to determine its factor of safety against sliding failure.

Materials Science: Developing Advanced Materials

Shear strain analysis is not only important in design but also plays a crucial role in the field of materials science. By understanding the shear properties of materials, scientists can develop new and improved materials for various engineering applications.

Characterization of Material Properties

Shear strain measurements are essential for characterizing the shear properties of materials. These properties include the shear modulus, shear strength, and shear ductility, which are critical for predicting material behavior under shear loading.

Experimental techniques, such as torsion tests and shear tests, are used to measure the shear stress-strain relationship of materials. This data is used to develop material models and to validate the performance of materials in engineering applications.

Development of New Materials

Understanding shear strain behavior aids in the development of new materials with improved shear resistance. By manipulating the microstructure and composition of materials, scientists can enhance their ability to withstand shear stresses and strains.

For example, composite materials are often designed with specific fiber orientations to maximize their shear strength and stiffness. Shear strain analysis is used to optimize the design of these composites to achieve the desired mechanical properties.

Geology (Geophysics): Predicting Seismic Activity

In geology and geophysics, shear strain measurements contribute significantly to understanding geological phenomena, particularly concerning fault lines and seismic activity. This understanding is crucial for predicting and mitigating the impact of earthquakes.

Fault Lines and Seismic Activity

Earthquakes occur when the shear stress along a fault line exceeds the fault's shear strength, causing a sudden release of energy. Shear strain measurements around fault lines provide valuable information about the accumulation of stress and the potential for seismic activity.

By monitoring the shear strain in the Earth's crust, geologists can identify areas where stress is building up and assess the likelihood of future earthquakes. This information is used to develop earthquake early warning systems and to implement building codes that improve the resilience of structures in earthquake-prone regions.

Solid Mechanics: Providing a Theoretical Foundation

Solid mechanics provides the theoretical framework for understanding the behavior of deformable solids, including the analysis of shear strain. The principles of solid mechanics are used to develop mathematical models that describe the relationship between stress, strain, and material properties.

Theoretical Framework

Solid mechanics provides the theoretical basis for understanding how materials deform under shear stress. It establishes the fundamental equations that relate shear stress to shear strain, taking into account material properties such as the shear modulus.

These theoretical models are essential for developing accurate computational simulations and for interpreting experimental data. The theory of elasticity, for example, provides a framework for analyzing the shear deformation of materials under small strain conditions.

Structural Analysis: Determining Stresses and Strains

Structural analysis utilizes various methods to determine stresses and strains in structures, ensuring they can withstand applied loads without failure. These methods range from analytical calculations to sophisticated numerical simulations.

Methods for Determining Stresses and Strains

Methods for determining stresses and strains in structures include:

• Analytical Methods: These methods involve using classical mechanics and mathematical equations to calculate stresses and strains in simple structures with well-defined geometries and loading conditions.
• Numerical Methods: Numerical methods, such as the finite element method (FEM), are used to analyze complex structures with irregular geometries and loading conditions. FEM divides the structure into small elements and solves the equations of equilibrium for each element, providing an approximate solution for the stress and strain distribution.

Both analytical and numerical methods are essential tools for structural engineers, allowing them to design safe and efficient structures that can withstand the demands of their intended use. By understanding the shear strain behavior of materials and structures, engineers can make informed decisions that ensure the safety and reliability of engineering systems.

Tools and Techniques for Shear Strain Analysis: From FEA to Strain Gauges

Shear strain is a fundamental concept in understanding how materials behave under stress. It specifically quantifies the deformation resulting from tangential, or shear, forces. This section will explore the diverse applications of shear strain analysis across various engineering fields. Now, let's examine the analytical tools and experimental techniques used to quantify and analyze this crucial phenomenon, from computational simulations to physical measurements.

Finite Element Analysis (FEA) for Shear Strain

Finite Element Analysis (FEA) stands as a cornerstone of modern engineering. It provides a powerful computational approach to simulate material behavior under a wide array of loading conditions, including shear. By dividing a complex structure into smaller, manageable elements, FEA allows engineers to predict stress and strain distributions with remarkable accuracy.

Advantages of FEA in Shear Analysis

FEA excels in handling complex geometries and material nonlinearities, which are often encountered in real-world engineering problems. It allows for detailed analysis of stress concentrations, identifying critical areas prone to failure under shear loading. Furthermore, FEA enables engineers to explore various design iterations and optimize material usage before physical prototypes are even created.

Limitations and Considerations

Despite its strengths, FEA is not without limitations. The accuracy of FEA results is highly dependent on the quality of the mesh, requiring careful consideration of element size and type. Computational cost can also be a significant factor, especially for large and complex models. Moreover, FEA results should always be validated with experimental data to ensure accuracy and reliability.

FEA Software for Shear Strain Analysis

A range of sophisticated FEA software packages are available to engineers. These packages provide the tools needed to define material properties, apply boundary conditions, and solve complex shear strain problems. Examples include:

• ANSYS: A widely used general-purpose FEA software known for its comprehensive capabilities and robust solver technology.

• Abaqus: Another leading FEA software package renowned for its advanced material modeling capabilities and ability to handle highly nonlinear problems.

• COMSOL: A multiphysics simulation platform that allows for the integration of various physical phenomena, including structural mechanics and heat transfer, in shear strain analysis.

Experimental Shear Strain Measurement with Strain Gauges

While FEA provides valuable insights through simulation, experimental techniques are essential for validating computational models and characterizing material behavior. Strain gauges are indispensable tools for direct measurement of strain in materials subjected to shear forces.

How Strain Gauges Work

Strain gauges are small, resistive sensors that are bonded to the surface of a material. When the material deforms under shear stress, the strain gauge also deforms, causing a change in its electrical resistance. This change in resistance is directly proportional to the strain, allowing for accurate measurement of shear strain.

Types and Applications of Strain Gauges

Different types of strain gauges are available to suit various applications. Foil strain gauges are commonly used for general-purpose strain measurement, while semiconductor strain gauges offer higher sensitivity for measuring small strains. Rosette strain gauges are specifically designed to measure strain in multiple directions, enabling the determination of shear strain components.

Shear Testing with Universal Testing Machines

Universal Testing Machines (UTMs) provide a controlled laboratory environment for applying shear forces and measuring the resulting strain. These machines allow engineers to perform standardized shear tests, such as torsion tests and shear punch tests, to characterize the shear properties of materials.

Controlled Laboratory Conditions

UTMs offer precise control over loading parameters, enabling researchers to investigate the effects of different loading rates and temperatures on shear strain behavior. The data obtained from UTM tests can be used to validate FEA models, refine material properties, and ensure the structural integrity of engineering designs.

Video: Shear Strain Formula: A Practical Guide Explained

Play Video

So, there you have it! Hopefully, this guide has demystified the shear strain formula and given you the confidence to tackle your own engineering challenges. Now, go forth and strain some…materials, responsibly of course!