Wavelength Units: The Ultimate Guide You Need to Know!
Electromagnetic radiation, a fundamental concept in physics, possesses a key characteristic: its wavelength. The quantitative measure of this wavelength is expressed using wavelength units, enabling precise communication and understanding across various scientific and technological disciplines. Spectroscopy, a powerful analytical technique, relies heavily on the accurate determination of wavelength units to analyze the composition and properties of matter. The nanometer (nm) serves as a commonly used wavelength units for describing visible and ultraviolet light. These wavelength units also play a critical role in the development of fiber optic communication, impacting bandwidth of data transmission.
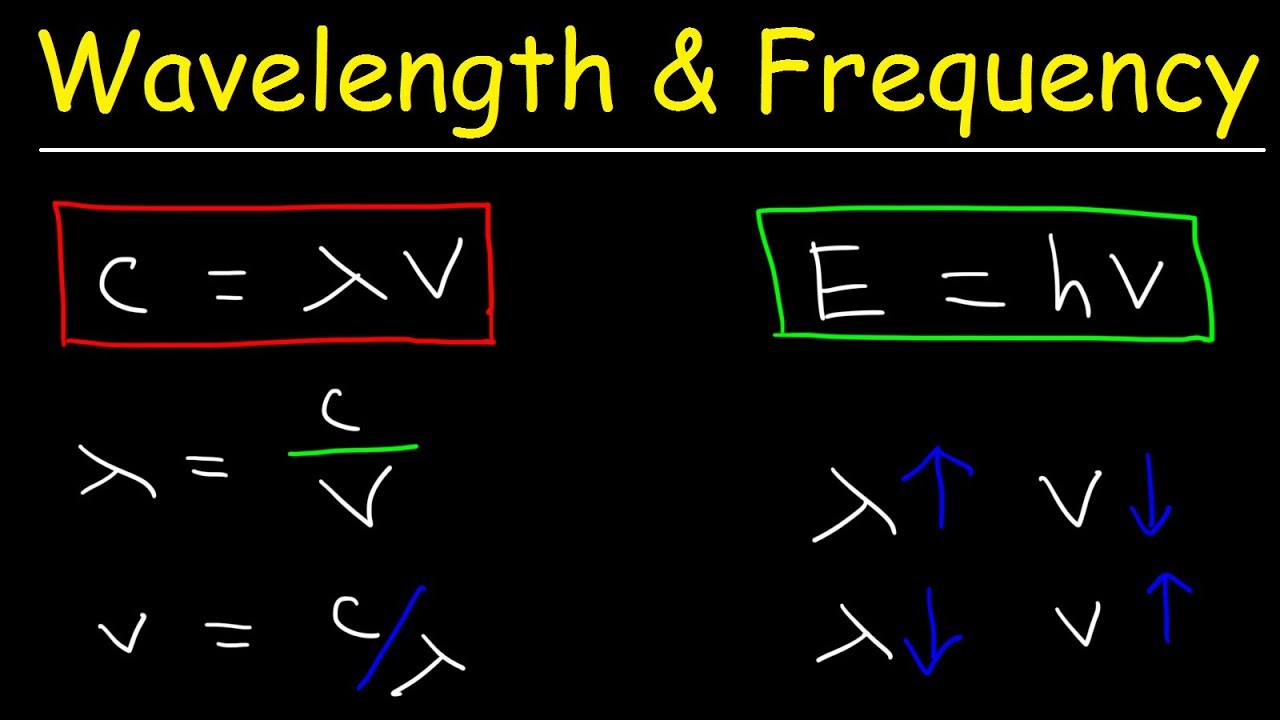
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Speed of Light, Frequency, and Wavelength Calculations - Chemistry Practice Problems .
Wavelength, a fundamental property of waves, dictates much of the behavior of light, sound, and other forms of energy propagation. Understanding what a wavelength is and the units used to measure it, is critical for navigating a range of scientific and technological disciplines. This section serves as an introduction to the concept, laying the groundwork for exploring its diverse applications and the significance of its measurement.
Defining Wavelength: The Distance of a Wave Cycle
At its core, wavelength is the spatial period of a wave – the distance over which the wave's shape repeats. Imagine a ripple in a pond; the wavelength is the distance from one crest to the next, or from one trough to the next. It represents one complete cycle of the wave.
This distance is typically measured in units of length, such as meters, centimeters, or nanometers, depending on the type of wave being observed. The shorter the wavelength, the more cycles occur within a given distance. Conversely, longer wavelengths correspond to fewer cycles.
Importance of Wavelength Units: A Key to Understanding the Universe
The precise measurement of wavelength is crucial in many fields because it provides insight into the nature and behavior of waves. Different phenomena can be precisely described and understood by using specific wavelength values.
In telecommunications, for instance, the wavelengths of radio waves and microwaves determine the frequencies at which information can be transmitted. In medicine, the wavelengths of X-rays and gamma rays dictate their ability to penetrate tissues for imaging or therapeutic purposes.
Furthermore, the correct units must be used to ensure accurate communication and prevent errors in calculations or applications. A misunderstanding of wavelength units could lead to misdiagnosis in medicine or failure in communication systems.
Without standardized units and a firm grasp of their meaning, scientific progress would be significantly hampered.
Brief Overview of the Electromagnetic Spectrum: A Glimpse of What’s Ahead
Wavelengths are perhaps most famously associated with the electromagnetic spectrum, which encompasses the entire range of electromagnetic radiation. This includes everything from radio waves, which can be several meters long, to gamma rays, which have wavelengths smaller than an atom.
The electromagnetic spectrum is a continuum, and each region within it—radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays—is defined by its specific range of wavelengths and frequencies. Each region interacts with matter in unique ways, leading to diverse applications in technology, medicine, and scientific research. Exploring this spectrum provides a fascinating insight into the power and versatility of wavelengths.
Common Wavelength Units: From Nanometers to Meters
Having established the fundamental concept of wavelength, it's time to explore the specific units used to quantify this property across different scales. The choice of unit depends largely on the context, with some units more suited to measuring extremely short wavelengths, such as those found in the atomic realm, and others better suited for macroscopic distances.
This section will delve into the definitions, significance, and practical applications of the most commonly used wavelength units, ranging from nanometers to meters, providing concrete examples to illustrate their relevance.
Nanometer (nm)
Definition and Significance
The nanometer (nm), equal to one billionth of a meter (10-9 m), is a unit of length primarily used to measure incredibly small distances. Its significance lies in its relevance to the atomic and molecular scale. At this level, the wave-like behavior of matter becomes pronounced, and dimensions are often expressed in nanometers.
Nanotechnology, materials science, and semiconductor manufacturing all heavily rely on the nanometer scale. Understanding and manipulating materials at this scale allows for the creation of novel devices and materials with enhanced properties.
Application in Atomic Scale Measurement
Nanometers are indispensable for describing the size of individual atoms, molecules, and nanoscale structures. For example, the diameter of a carbon nanotube, a cylindrical molecule with exceptional strength and electrical conductivity, is typically measured in nanometers.
Similarly, the size of features on a microchip, which dictate its processing power and efficiency, are also specified in nanometers. The ability to control dimensions at the nanometer scale is what drives innovation in electronics and other high-tech fields.
Micrometer (µm)
Definition and Significance
The micrometer (µm), also known as a micron, is equal to one millionth of a meter (10-6 m). It bridges the gap between the nanoscale and the macroscopic world. While still relatively small, the micrometer is large enough to describe the size of many biological cells, fibers, and other microscopic objects.
Its applications are diverse, spanning from biology and medicine to materials science and environmental monitoring. The micrometer provides a convenient unit for characterizing objects that are too small to be seen with the naked eye, yet too large to be effectively measured in nanometers.
Application in Measuring Bacteria Size
A prime example of the micrometer's utility is in measuring the size of bacteria. Most bacteria range in size from 0.5 to 5 micrometers. For instance, Escherichia coli (E. coli), a common bacterium found in the human gut, typically has a length of around 2 micrometers.
Microscopists routinely use micrometers to quantify the size and shape of microorganisms, aiding in their identification and classification. This is crucial for diagnosing infections, understanding microbial ecology, and developing new antimicrobial therapies.
Millimeter (mm)
Definition and Significance
The millimeter (mm), equivalent to one thousandth of a meter (10-3 m), is a more familiar unit of length encountered in everyday life. It represents a scale at which objects become easily visible to the naked eye. Millimeters are commonly used in engineering, manufacturing, and construction for precise measurements of small objects.
Its significance lies in its accessibility and practicality. Rulers, calipers, and other measuring instruments are often calibrated in millimeters, making it a convenient unit for many applications.
Application in Measuring Small Objects
Millimeters are frequently used to measure the dimensions of small manufactured parts, such as screws, bolts, and electronic components. For instance, the diameter of a small screw might be specified as 4 mm, while the thickness of a sheet of metal could be 0.8 mm.
In the medical field, millimeters are used to measure the size of skin lesions, tumors, and other anatomical features. This level of precision is essential for accurate diagnosis and treatment planning.
Centimeter (cm)
Definition and Significance
The centimeter (cm), equal to one hundredth of a meter (10-2 m), is another commonly used unit in everyday measurements. It's larger than a millimeter, making it suitable for describing the size of slightly larger objects. Centimeters are prevalent in clothing sizes, household item dimensions, and basic construction.
Its significance lies in its ease of use and its direct relationship to the meter. Many rulers and measuring tapes feature both centimeters and inches, providing flexibility for different measurement preferences.
Application in Daily Objects
Centimeters are routinely used to measure the height and width of picture frames, the length of pencils, and the diameter of plates. For example, a standard sheet of paper is 21 cm wide, and a typical drinking glass might have a diameter of 8 cm.
In tailoring and sewing, centimeters are used to measure fabric lengths, body dimensions, and seam allowances. Its frequent use in these areas showcases the unit's practicality in our daily routines.
Meter (m)
Definition and Significance
The meter (m) is the base unit of length in the International System of Units (SI). It is a fundamental unit used to measure distances in a wide variety of contexts, from the height of a person to the length of a room.
Its significance stems from its role as the cornerstone of the metric system, providing a standardized and universally accepted unit of length. It is crucial in construction, sports, and large-scale manufacturing.
Application in Measuring Distance
Meters are used to measure the height of buildings, the length of running tracks, and the dimensions of furniture. For example, a standard doorway is typically around 2 meters high, and a soccer field is approximately 100 meters long.
In navigation and surveying, meters are used to measure distances between landmarks, elevation changes, and geographical coordinates. The meter is crucial in any field where larger distance quantification is important.
Angstrom (Å)
Definition and Significance
The Angstrom (Å), equal to 10-10 meters (0.1 nm), is a unit of length primarily used in chemistry, solid-state physics, and structural biology to express the sizes of atoms and the distances between them in molecules and crystals. Although not an SI unit, it remains in use due to its convenience in describing atomic-scale phenomena.
Its significance is in its ability to provide an intuitive scale for these incredibly small dimensions. It is particularly useful when dealing with interatomic distances, bond lengths, and the wavelengths of X-rays used in crystallography.
Application in Measuring Atomic Radius
Angstroms are frequently used to express the radii of atoms and ions. For example, the radius of a hydrogen atom is approximately 0.53 Å, while the length of a typical carbon-carbon bond in an organic molecule is around 1.5 Å.
In X-ray crystallography, the wavelengths of X-rays used to determine the structure of crystals are also typically expressed in Angstroms. The ability to measure and describe these dimensions with precision is crucial for understanding the properties of materials at the atomic level.
Having explored the individual units used to measure wavelength, from the incredibly small nanometer to the more macroscopic meter, it's time to zoom out and view these units within the context of a much larger framework: the electromagnetic spectrum. This spectrum encompasses the entire range of electromagnetic radiation, from extremely long radio waves to incredibly short gamma rays, and understanding its organization is crucial for appreciating the diverse ways in which wavelengths manifest in our universe.
The Electromagnetic Spectrum: A Wavelength Wonderland
The electromagnetic spectrum is a continuous range of all types of electromagnetic radiation. It's a comprehensive map that organizes these radiations based on their frequency and, more importantly for our discussion, their wavelength. Imagine it as a vast ocean of energy, where each wave has a unique size, dictating its behavior and interaction with matter.
The electromagnetic spectrum spans an enormous range, from wavelengths longer than skyscrapers to those smaller than atomic nuclei. This vast difference in scale leads to dramatically different properties and applications.
The spectrum is not a collection of discrete, separate entities. Instead, it is a continuous spectrum where one type of radiation gradually blends into the next. There are no sharp dividing lines, only regions characterized by specific wavelength ranges.
Arrangement by Wavelength and Frequency
The arrangement of the electromagnetic spectrum is fundamentally based on the inverse relationship between wavelength and frequency. As wavelength increases, frequency decreases, and vice versa. This relationship is governed by the speed of light, a constant that links these two properties.
It's crucial to remember that higher frequency means shorter wavelength, and lower frequency corresponds to longer wavelength. This relationship dictates the energy associated with each type of radiation. Shorter wavelengths (and thus higher frequencies) carry more energy than longer wavelengths.
Regions of the Spectrum and Their Wavelengths
The electromagnetic spectrum is conventionally divided into several distinct regions, each characterized by a specific range of wavelengths and frequencies. These regions, while arbitrarily defined, are useful for categorizing and understanding the diverse properties of electromagnetic radiation.
Radio Waves
Radio waves occupy the longest wavelength portion of the spectrum, ranging from millimeters to hundreds of kilometers.
They are used extensively in communication technologies, including broadcasting, mobile phones, and satellite communication. Their long wavelengths allow them to propagate over long distances and penetrate obstacles, making them ideal for transmitting signals.
Infrared Radiation
Infrared radiation falls between microwaves and visible light on the spectrum, with wavelengths ranging from approximately 700 nanometers to 1 millimeter.
We experience infrared radiation as heat. It's used in thermal imaging, remote controls, and industrial heating applications.
Visible Light
Visible light occupies a very narrow band in the middle of the electromagnetic spectrum, ranging from approximately 400 nanometers (violet) to 700 nanometers (red).
This is the only portion of the spectrum that is visible to the human eye. Different wavelengths within this range are perceived as different colors.
Ultraviolet Radiation
Ultraviolet (UV) radiation has shorter wavelengths than visible light, ranging from approximately 10 nanometers to 400 nanometers.
UV radiation carries more energy than visible light and can be harmful to living organisms. It's responsible for sunburns and can contribute to skin cancer. However, it also has beneficial uses, such as in sterilization and vitamin D production.
X-rays
X-rays have even shorter wavelengths, ranging from approximately 0.01 nanometers to 10 nanometers.
Their ability to penetrate soft tissues makes them invaluable in medical imaging, allowing doctors to visualize bones and internal organs. However, prolonged exposure to X-rays can be harmful due to their ionizing radiation.
Gamma Rays
Gamma rays have the shortest wavelengths and highest energies in the electromagnetic spectrum.
They are produced by nuclear reactions and radioactive decay. Gamma rays are used in radiation therapy to treat cancer, but they are also highly dangerous due to their ionizing properties.
Having explored the individual units used to measure wavelength, from the incredibly small nanometer to the more macroscopic meter, it's time to zoom out and view these units within the context of a much larger framework: the electromagnetic spectrum. This spectrum encompasses the entire range of electromagnetic radiation, from extremely long radio waves to incredibly short gamma rays, and understanding its organization is crucial for appreciating the diverse ways in which wavelengths manifest in our universe.
Wavelength, Frequency, and Energy: The Interconnected Trio
Wavelength isn't an isolated property. It exists in a dynamic relationship with both frequency and energy. Understanding these interconnected parameters is key to grasping the true nature of electromagnetic radiation. Let's delve into how these properties intertwine.
The Inverse Relationship Between Wavelength and Frequency
Wavelength and frequency are inversely proportional. This means that as one increases, the other decreases, and vice versa.
Imagine a rope being shaken to create waves. If you shake it slowly, you create long wavelengths with a low frequency (fewer waves passing a point per second). If you shake it rapidly, you create short wavelengths with a high frequency (more waves passing a point per second).
This fundamental relationship is critical in understanding the behavior of all electromagnetic radiation.
Explaining Hertz (Hz) as a Unit of Frequency
Frequency is measured in Hertz (Hz), named after the German physicist Heinrich Hertz.
One Hertz (1 Hz) represents one cycle per second. Therefore, a wave with a frequency of 10 Hz completes 10 cycles every second.
Higher frequencies, such as those used in radio transmission, are often expressed in kilohertz (kHz, 1000 Hz), megahertz (MHz, 1,000,000 Hz), or gigahertz (GHz, 1,000,000,000 Hz).
Understanding Hertz is essential for quantifying the rate at which waves oscillate, directly influencing their properties and applications.
The Role of Speed of Light (c)
The speed of light (c) is a universal constant that plays a crucial role in connecting wavelength and frequency. In a vacuum, light travels at approximately 299,792,458 meters per second (often rounded to 3.0 x 108 m/s).
This constant speed dictates the relationship between how long a wave is (wavelength) and how often it oscillates (frequency). It is the bridge between these two fundamental properties.
The Formula: c = λν (Speed of Light = Wavelength x Frequency)
The relationship between the speed of light (c), wavelength (λ, lambda), and frequency (ν, nu) is expressed by the formula:
c = λν
Where:
- c is the speed of light (approximately 3.0 x 108 m/s)
- λ is the wavelength (in meters)
- ν is the frequency (in Hertz)
This formula tells us that the speed of light is equal to the product of wavelength and frequency.
We can rearrange this formula to solve for either wavelength or frequency if the other is known:
- λ = c / ν (Wavelength = Speed of Light / Frequency)
- ν = c / λ (Frequency = Speed of Light / Wavelength)
Using the Formula
For example, if a radio wave has a frequency of 100 MHz (100,000,000 Hz), we can calculate its wavelength:
λ = (3.0 x 108 m/s) / (100 x 106 Hz) = 3 meters.
This formula is not just a theoretical construct; it is a powerful tool used by scientists and engineers to design and analyze systems that utilize electromagnetic radiation, from radio communication to medical imaging.
Having explored the intricate relationship between wavelength, frequency, and energy, it's natural to focus our attention on the portion of the electromagnetic spectrum that is most familiar to us: visible light. This narrow band of radiation, detectable by the human eye, is responsible for the rich tapestry of colors that surrounds us. It's where the concept of wavelength takes on a uniquely aesthetic dimension.
Visible Light: A Symphony of Wavelengths
The realm of visible light represents a tiny sliver within the vast electromagnetic spectrum, yet it's arguably the most crucial for our everyday experience. Each specific wavelength within this range corresponds to a distinct color, a phenomenon that underpins our perception of the world.
The Visible Spectrum: A Colorful Palette of Wavelengths
The visible spectrum typically spans wavelengths from approximately 380 nanometers (nm) to 750 nm. This range contains all the colors that humans can perceive. At the shorter end of the spectrum, around 380-450 nm, we find violet light. Moving towards longer wavelengths, we encounter blue (450-495 nm), green (495-570 nm), yellow (570-590 nm), orange (590-620 nm), and finally, red (620-750 nm).
It is crucial to note that these are approximate ranges. There is some overlap between colors. The perceived color can also be affected by the intensity of the light and the surrounding colors.
Think of a rainbow: this natural phenomenon provides a stunning visual representation of the visible spectrum. Sunlight refracts through water droplets, separating the light into its constituent wavelengths and displaying the continuous gradient of colors.
How Wavelength Affects Color Perception
The human eye contains specialized cells called cone cells, located in the retina. These cells are responsible for color vision.
There are three main types of cone cells, each sensitive to different ranges of wavelengths: short (S) cones, which are most sensitive to blue light; medium (M) cones, which are most sensitive to green light; and long (L) cones, which are most sensitive to red light.
When light enters the eye, it stimulates these cone cells to varying degrees, depending on the wavelengths present in the light. The brain then interprets the relative activation levels of the three types of cones to perceive a specific color.
For example, if light with a wavelength of 530 nm enters the eye, it will primarily stimulate the M cones (green). The brain will interpret this signal as green.
If light stimulates both the L and M cones equally, the brain perceives yellow.
The brain's interpretation of color is therefore a complex process involving the differential activation of these cone cells. Furthermore, the perceived color can also be influenced by contextual factors. These factors includes the surrounding colors, the adaptation of the eye to different lighting conditions, and even individual differences in color vision.
Having explored the intricate relationship between wavelength, frequency, and energy, it's natural to focus our attention on the portion of the electromagnetic spectrum that is most familiar to us: visible light. This narrow band of radiation, detectable by the human eye, is responsible for the rich tapestry of colors that surrounds us. It's where the concept of wavelength takes on a uniquely aesthetic dimension.
Wavelength in Action: Diverse Applications Across Fields
The abstract concept of wavelength transforms into concrete utility when we examine its diverse applications across various fields. From the invisible signals that connect us globally to the life-saving tools used in medicine and the methods astronomers use to unravel cosmic mysteries, wavelength plays a pivotal role. Let's explore some key examples.
Telecommunications: Riding the Radio Waves and Microwaves
Telecommunications relies heavily on radio waves and microwaves, both of which occupy different regions of the electromagnetic spectrum, with radio waves having the longer wavelengths. The wavelength of these waves directly dictates their properties and suitability for different communication technologies.
Radio waves, due to their longer wavelengths, can diffract around obstacles and travel long distances, making them ideal for broadcasting. AM radio, for example, utilizes longer wavelengths that can propagate over the horizon, allowing for signal reception even when the transmitter is not in direct line of sight.
Microwaves, with their shorter wavelengths, are used in satellite communications and wireless networking (Wi-Fi). Their shorter wavelengths allow for higher bandwidth, meaning they can carry more data. This makes them suitable for transmitting large amounts of information quickly and efficiently.
The development of 5G technology represents a significant advancement in telecommunications, with even shorter wavelengths being utilized to increase data transfer speeds. However, these shorter wavelengths are more susceptible to interference and require a denser network of base stations to ensure reliable coverage.
The strategic use of varying wavelengths allows telecommunication companies to tailor their technologies to specific needs, whether it's broadcasting signals across vast distances or transmitting massive amounts of data at high speeds.
Medicine: Harnessing X-rays and Gamma Radiation for Imaging and Treatment
In medicine, the shorter, more energetic wavelengths of X-rays and gamma radiation are indispensable for both diagnostic imaging and therapeutic treatment. X-rays, with their ability to penetrate soft tissues, are used in radiography to visualize bones and other dense structures.
The contrast in X-ray images is achieved through differential absorption of the radiation by different tissues. Dense materials like bone absorb more X-rays, appearing white on the image, while less dense tissues allow more X-rays to pass through, appearing darker.
Computed Tomography (CT) scans utilize X-rays to create detailed cross-sectional images of the body, providing a more comprehensive view than traditional X-rays. These scans are crucial for diagnosing a wide range of conditions, from bone fractures to internal bleeding.
Gamma radiation, with its even shorter wavelengths and higher energy, is used in radiation therapy to target and destroy cancerous cells. Focused beams of gamma rays are directed at tumors, damaging the DNA of cancer cells and preventing them from multiplying.
While radiation therapy can be highly effective, it also carries the risk of damaging healthy tissues. Therefore, precise targeting and careful dosage are essential to minimize side effects.
The use of different wavelengths allows medical professionals to visualize the inner workings of the body and target diseases with precision.
Astronomy: Decoding the Light from Stars and Galaxies
Astronomy relies heavily on analyzing the light emitted by celestial objects to understand their composition, distance, and motion. Each element emits and absorbs light at specific wavelengths, creating a unique spectral fingerprint.
By analyzing the spectrum of light from a star, astronomers can determine its chemical composition, temperature, and velocity. This process, known as spectroscopy, is a fundamental tool in astrophysics.
The Doppler effect, which causes a shift in wavelength depending on the relative motion of the source and observer, is also used to measure the speed at which stars and galaxies are moving towards or away from us. A blueshift indicates motion towards us, while a redshift indicates motion away.
Different wavelengths of light reveal different aspects of celestial objects. For example, infrared telescopes can penetrate dust clouds that obscure visible light, allowing astronomers to study star formation regions.
Radio telescopes detect radio waves emitted by galaxies and other cosmic sources, providing information about their magnetic fields and the distribution of gas and dust. X-ray telescopes detect X-rays emitted by black holes and other high-energy phenomena, providing insights into the most extreme environments in the universe.
The multi-wavelength approach to astronomy allows for a comprehensive understanding of the cosmos, revealing the secrets of stars, galaxies, and the universe as a whole. By studying the universe across the electromagnetic spectrum, scientists gain a more complete understanding of its origins, evolution, and ultimate fate.
Video: Wavelength Units: The Ultimate Guide You Need to Know!
Frequently Asked Questions About Wavelength Units
This FAQ section addresses common questions regarding wavelength units discussed in the "Wavelength Units: The Ultimate Guide You Need to Know!" article. We aim to provide clear and concise answers to help you better understand these concepts.
What are the most common wavelength units?
The most commonly used wavelength units are meters (m), centimeters (cm), millimeters (mm), micrometers (µm), nanometers (nm), and Ångströms (Å). Nanometers are especially prevalent when dealing with visible light and ultraviolet radiation, while meters are more suited for radio waves. Choosing the right unit simplifies calculations and comparisons.
Why are smaller wavelength units like nanometers often preferred?
Smaller wavelength units, such as nanometers, are favored because they provide convenient numerical values when expressing the wavelengths of light and other electromagnetic radiation. Using meters for these wavelengths would result in very small decimal numbers, making them less practical. It streamlines scientific communication and data representation.
How do I convert between different wavelength units?
To convert between different wavelength units, you need to understand the relationship between them. For example, 1 meter equals 1,000,000,000 nanometers. Use conversion factors or online tools to accurately convert between wavelength units such as meters to nanometers, or micrometers to millimeters.
Are there any specific industries that heavily rely on precise wavelength units?
Yes, several industries rely heavily on precise wavelength units. These include telecommunications (fiber optics), spectroscopy (analyzing light spectra), semiconductor manufacturing (lithography), and medical imaging (MRI, X-ray). Accurate measurement and control of wavelength units are crucial for ensuring the functionality and precision of the tools and technologies used in these sectors.
