Units of Angular Momentum: The Ultimate Guide [Explained]
Angular momentum, a fundamental concept in physics, finds its quantitative expression through units for angular momentum. The International System of Units (SI) defines the standard unit for angular momentum as kilograms meters squared per second (kg⋅m²/s). Understanding these units for angular momentum is crucial in fields ranging from quantum mechanics, where the angular momentum of particles dictates their behavior, to astronomy, where celestial bodies exhibit significant angular momentum. Similarly, precise knowledge of units for angular momentum also aids the work of organization such as NASA in their trajectory and attitude determination for spacecraft. The relevance of the units for angular momentum can also be noted in the works of physics luminaries such as Sir Isaac Newton, who first defined the foundational concepts of momentum and motion.
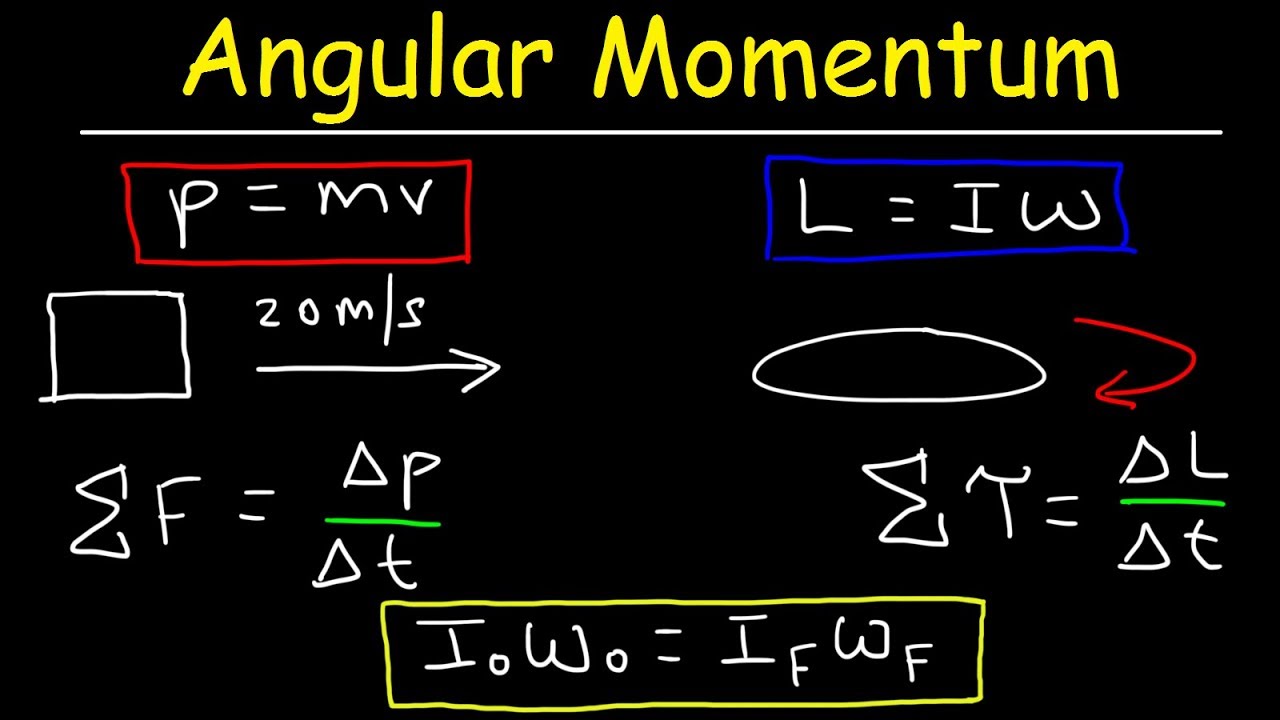
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Angular Momentum - Basic Introduction, Torque, Inertia, Conservation of Angular Momentum .
Imagine a figure skater gracefully spinning on the ice. As they pull their arms inward, their rotational speed dramatically increases. This captivating demonstration perfectly illustrates the principle of angular momentum – a fundamental concept governing the rotational motion of objects.
Angular momentum, in essence, is the rotational equivalent of linear momentum. While linear momentum describes an object's resistance to changes in its linear motion, angular momentum describes an object's resistance to changes in its rotational motion.
The Significance of Units
Understanding the units of angular momentum is crucial for a number of reasons. First, proper unit usage ensures accurate calculations and predictions in fields ranging from astrophysics to quantum mechanics. Second, consistent unit application enables clear communication and collaboration among scientists and engineers. Finally, a firm grasp of these units allows for a deeper, more intuitive understanding of the underlying physics at play.
What This Guide Will Cover
This guide serves as a comprehensive exploration of angular momentum units, designed to provide clarity and practical knowledge. We will start by defining angular momentum, relating it to key concepts like rotational inertia and angular velocity.
Then we will delve into the globally accepted SI units for angular momentum, dissecting each component and illustrating its derivation. We will explore the fascinating realm of quantum mechanics. This exploration will reveal how angular momentum is quantized at the atomic level.
Finally, we will examine real-world examples across diverse disciplines, highlighting the practical importance of understanding angular momentum units. By the end of this journey, you will have a solid foundation for confidently working with angular momentum and its units in various scientific and engineering contexts.
Imagine a figure skater gracefully spinning on the ice. As they pull their arms inward, their rotational speed dramatically increases. This captivating demonstration perfectly illustrates the principle of angular momentum – a fundamental concept governing the rotational motion of objects.
Angular momentum, in essence, is the rotational equivalent of linear momentum. While linear momentum describes an object's resistance to changes in its linear motion, angular momentum describes an object's resistance to changes in its rotational motion.
To truly grasp the intricacies of angular momentum and its units, a strong conceptual foundation is essential. Let's delve into the heart of this fascinating concept, exploring its definition, relationships, and key components.
Defining Angular Momentum: A Conceptual Foundation
What is Angular Momentum?
At its core, angular momentum is a measure of an object's tendency to continue rotating.
It quantifies the difficulty of stopping or changing the rotational motion of an object. Just as a heavier object is harder to stop in linear motion (due to its greater linear momentum), an object with greater angular momentum is harder to stop or alter in its rotation.
Angular momentum is a vector quantity, meaning it has both magnitude and direction. The direction of the angular momentum vector is perpendicular to the plane of rotation, determined by the right-hand rule.
Angular Momentum, Rotational Inertia, and Angular Velocity
Angular momentum is intrinsically linked to two other crucial concepts: rotational inertia and angular velocity.
Rotational inertia, also known as the moment of inertia, represents an object's resistance to changes in its rotational speed. It depends on the object's mass distribution relative to the axis of rotation.
Angular velocity, on the other hand, describes how fast an object is rotating.
The relationship between these three is fundamental: angular momentum is the product of rotational inertia and angular velocity. Increasing either the rotational inertia or the angular velocity of an object will increase its angular momentum.
Orbital vs. Spin Angular Momentum
It’s important to distinguish between two types of angular momentum: orbital and spin.
Orbital angular momentum is associated with the motion of an object around a fixed point or axis. Think of a planet orbiting a star – that's orbital angular momentum in action.
Spin angular momentum, on the other hand, is the angular momentum of an object rotating about its own axis. A spinning top exemplifies spin angular momentum.
Both types contribute to the total angular momentum of a system.
Understanding Moment of Inertia
As mentioned earlier, the moment of inertia (I) plays a critical role in determining angular momentum. It's not just the mass of an object, but how that mass is distributed around the axis of rotation.
An object with its mass concentrated further from the axis of rotation will have a higher moment of inertia, making it harder to start or stop its rotation.
Different shapes and mass distributions have different formulas for calculating the moment of inertia. For instance, a solid sphere has a different moment of inertia than a hollow sphere of the same mass and radius.
The Formula for Angular Momentum
The mathematical relationship between angular momentum (L), moment of inertia (I), and angular velocity (ω) is expressed by the simple yet powerful formula:
L = Iω
Where:
- L represents angular momentum.
- I represents the moment of inertia.
- ω represents angular velocity.
This formula highlights that angular momentum is directly proportional to both the moment of inertia and the angular velocity. A larger moment of inertia or a higher angular velocity will result in a larger angular momentum. This equation serves as the bedrock for understanding and calculating angular momentum in various physical scenarios.
Imagine a figure skater gracefully spinning on the ice. As they pull their arms inward, their rotational speed dramatically increases. This captivating demonstration perfectly illustrates the principle of angular momentum – a fundamental concept governing the rotational motion of objects.
Angular momentum, in essence, is the rotational equivalent of linear momentum. While linear momentum describes an object's resistance to changes in its linear motion, angular momentum describes an object's resistance to changes in its rotational motion.
To truly grasp the intricacies of angular momentum and its units, a strong conceptual foundation is essential. Where we clearly defined angular momentum and all of its components, now let's transition into understanding how we measure it.
The Standard: Angular Momentum in SI Units
In the world of scientific measurement, consistency and universality are paramount. This is where the International System of Units (SI) steps in, providing a globally accepted standard for expressing physical quantities. For angular momentum, the SI unit is the kilogram meter squared per second (kg m²/s). Let's delve into what this unit signifies and how it's derived.
Decoding the Kilogram Meter Squared Per Second (kg m²/s)
The seemingly complex unit of kg m²/s is actually built from simpler, fundamental units:
- Kilogram (kg): The base unit of mass, representing the amount of matter in an object.
- Meter (m): The base unit of length, representing distance.
- Second (s): The base unit of time.
The combination of these units into kg m²/s reflects the physical quantities that contribute to angular momentum. But how does this specific combination arise?
Deriving the Unit from the Formula L = Iω
The formula for angular momentum, L = Iω, provides the key to understanding the unit's derivation. Let's break down each component:
- L: Represents angular momentum.
- I: Represents the moment of inertia, which is the resistance of an object to rotational motion.
- ω: Represents angular velocity, which is the rate of change of angular position.
The moment of inertia (I) has units of kg m². This makes intuitive sense because it depends on both the mass of the object and the distribution of that mass relative to the axis of rotation. A greater mass further from the axis of rotation results in a greater moment of inertia.
Angular velocity (ω) is typically measured in radians per second (rad/s). While radians are dimensionless (a ratio of two lengths), it's important to include "per second" to represent the rate of rotation. Thus the formula, kg m² * rad/s = kg m²/s.
When we multiply the units of moment of inertia (kg m²) by the units of angular velocity (rad/s), we arrive at the SI unit for angular momentum: kg m²/s. Radian is considered unitless.
Therefore, multiplying the units together leads to the following relationship:
kg⋅m2⋅rad/s=kg⋅m2/s
Angular Momentum Values in Action
To solidify your understanding, let's consider a few examples of angular momentum values expressed in SI units:
-
A spinning figure skater might have an angular momentum of around 50 kg m²/s.
-
The Earth, as it orbits the Sun, has an immense angular momentum of approximately 1040 kg m²/s.
-
On a much smaller scale, an electron in an atom possesses quantized angular momentum, with values on the order of 10-34 kg m²/s. This is defined by the planck constant.
These examples illustrate the wide range of angular momentum values encountered in various physical systems, all consistently expressed using the SI unit of kg m²/s. This standardization allows scientists and engineers to compare and analyze rotational motion across diverse scales and applications.
Angular Momentum and Quantum Mechanics
Our exploration of angular momentum now takes us into the realm of the infinitesimally small: the world of atoms and subatomic particles. Here, classical mechanics, with its smooth, continuous descriptions, gives way to the often counter-intuitive, yet incredibly precise, rules of quantum mechanics.
The Quantum Revolution: Why Quantum Mechanics Matters
At the atomic level, angular momentum isn't just another physical quantity; it's a fundamental property that dictates the behavior of matter. Quantum mechanics reveals that angular momentum, like energy, is quantized, meaning it can only exist in discrete, specific values. This quantization has profound implications for understanding atomic structure, chemical bonding, and the behavior of matter in extreme conditions.
Classical physics fails to explain many phenomena observed at the atomic level. For example, why don't electrons, constantly accelerating as they orbit the nucleus, radiate energy and spiral into it? The answer lies in the quantization of angular momentum and energy, a cornerstone of quantum mechanics.
The Planck Constant: Quantifying the Quantum World
The bridge between classical and quantum angular momentum is the Planck constant, denoted by the symbol ħ (pronounced "h-bar"). This fundamental constant of nature, approximately equal to 1.054 × 10⁻³⁴ joule-seconds (J⋅s), governs the scale at which quantum effects become significant.
In the context of angular momentum, the Planck constant dictates the smallest possible unit of angular momentum. The allowed values of angular momentum are integer or half-integer multiples of ħ. This means an atom cannot have any arbitrary amount of angular momentum; it's restricted to specific, quantized levels.
Quantization of Angular Momentum: Discrete Steps
The quantization of angular momentum has a direct impact on the observable properties of atoms and molecules. For instance, the energy levels of an atom are directly related to the angular momentum of its electrons. Because angular momentum is quantized, the energy levels are also quantized, leading to distinct spectral lines when atoms absorb or emit light.
Consider an electron orbiting the nucleus of an atom. In classical physics, the electron could, in theory, have any amount of angular momentum.
However, quantum mechanics dictates that the electron's orbital angular momentum (L) is quantized according to the following equation:
L = √(l(l+1)) ħ
Where l is the orbital angular momentum quantum number, and can only take on integer values of 0, 1, 2, and so on. This quantum number determines the shape of the electron's orbital and its contribution to the atom's total angular momentum.
Example: Angular Momentum of an Electron in an Atom
Let's delve into a specific example: the angular momentum of an electron in a hydrogen atom. The electron occupies specific orbitals, each characterized by a set of quantum numbers, including the orbital angular momentum quantum number (l).
For an electron in an s orbital (l = 0), the orbital angular momentum is zero. This might seem counterintuitive, but it reflects the spherical symmetry of the s orbital.
For an electron in a p orbital (l = 1), the orbital angular momentum is √(2) ħ. This non-zero angular momentum contributes to the atom's overall magnetic moment and influences its interactions with external magnetic fields.
Moreover, electrons also possess spin angular momentum, an intrinsic property analogous to a tiny spinning top. Electron spin is also quantized, with a spin quantum number of s = 1/2. This means an electron's spin angular momentum is always √(3/4) ħ.
The total angular momentum of an atom is the vector sum of the orbital and spin angular momenta of all its electrons. This total angular momentum is also quantized and plays a crucial role in determining the atom's spectroscopic properties and chemical behavior. The consequences of angular momentum quantization are observed in various spectroscopic techniques, where atoms absorb or emit photons of specific energies, creating characteristic spectral patterns.
Of course! Here is the expanded section of the outline, written as a standalone analytical editorial-style article section.
Practical Applications and Examples
The abstract world of angular momentum units may seem far removed from everyday life, but its principles are deeply embedded in a wide range of disciplines. From the grand scale of celestial mechanics to the intricate workings of atomic physics, a firm grasp of angular momentum and its units is essential for accurate modeling, analysis, and technological advancement. Let's explore some compelling real-world examples.
Astrophysics: Unveiling the Cosmos
Astrophysics offers a breathtaking canvas for the application of angular momentum principles. Consider planetary rotation: each planet in our solar system possesses angular momentum, dictating its rotational speed and orientation. Understanding this angular momentum, quantified in kg m²/s, helps us model the stability of planetary orbits and the dynamics of day-night cycles.
Galaxy formation is another area where angular momentum reigns supreme. The swirling, majestic spiral arms of galaxies are a direct consequence of the conservation of angular momentum during their formation. The distribution of mass and the rate of rotation within a galaxy are intimately linked to its total angular momentum. Without accurate measurements and calculations involving angular momentum units, our understanding of galactic evolution would be severely limited.
Engineering: Harnessing Rotational Power
In the realm of engineering, angular momentum finds practical application in numerous devices and systems. Flywheels, for instance, are ingenious mechanical components designed to store rotational energy. The amount of energy a flywheel can store is directly proportional to its moment of inertia and the square of its angular velocity, both of which are expressed using angular momentum units.
Rotating machinery, from turbines in power plants to rotors in helicopters, also relies heavily on angular momentum principles. Engineers must carefully consider the angular momentum of rotating components to ensure stability, prevent excessive vibrations, and optimize performance. An imbalance in angular momentum can lead to catastrophic failures, highlighting the critical importance of precise calculations and a deep understanding of the relevant units.
Quantum Mechanics: Probing the Subatomic World
The peculiar laws of quantum mechanics reveal angular momentum in an entirely new light. In the realm of atoms and subatomic particles, angular momentum is quantized, meaning it can only exist in discrete, specific values. This quantization has profound consequences for the behavior of matter at the most fundamental level.
Spectroscopy, a powerful technique used to analyze the composition and properties of materials, relies heavily on understanding the angular momentum of electrons within atoms. When atoms absorb or emit light, electrons transition between energy levels with different angular momentum values. The frequencies of light absorbed or emitted are directly related to these angular momentum transitions, providing a unique fingerprint for each element and molecule.
Atomic physics, the study of the structure and behavior of atoms, is intrinsically linked to angular momentum. The arrangement of electrons within an atom, which dictates its chemical properties, is determined by the allowed values of their angular momentum. Quantum mechanics predicts that the angular momentum of an electron in an atom is quantized. These concepts are crucial for understanding chemical bonding, molecular structure, and the behavior of materials under extreme conditions.
Video: Units of Angular Momentum: The Ultimate Guide [Explained]
FAQs: Units of Angular Momentum
Here are some frequently asked questions to clarify the concept of angular momentum and its units.
What are the most common units for angular momentum?
The most common units for angular momentum are kilogram meters squared per second (kg⋅m²/s) in the International System of Units (SI). In the CGS system, the unit is gram centimeter squared per second (g⋅cm²/s). Understanding these units is crucial for calculations.
Why is angular momentum often expressed in different units?
While kg⋅m²/s is the standard, other units sometimes appear, particularly in specialized fields. These can include variations that incorporate other related quantities like energy or time. It's always important to carefully examine the context to understand the units being used.
How are the units for angular momentum derived?
Angular momentum (L) is calculated as L = r x p, where r is the position vector and p is the linear momentum. Since linear momentum's units are kg⋅m/s, and the position vector's units are meters, their product yields kg⋅m²/s as the units for angular momentum.
Are there any dimensionless units for angular momentum?
In quantum mechanics, angular momentum is often expressed in units of ħ (h-bar), which is the reduced Planck constant. While ħ itself has units of energy multiplied by time (J⋅s), expressing angular momentum in multiples of ħ effectively makes it dimensionless in some contexts, simplifying certain quantum calculations.