Rolling Without Slipping Formula: A Practical Guide

The rolling without slipping condition represents a fundamental concept in classical mechanics, particularly when analyzing the motion of rigid bodies. This constraint dictates a precise relationship between the linear velocity of the center of mass and the angular velocity around the center of mass; specifically, for a wheel of radius r rolling on a surface, the linear speed (v) is equivalent to the product of the angular speed (ω) and the radius (r), as expressed in the rolling without slipping formula: v = rω. The Massachusetts Institute of Technology (MIT) routinely incorporates problems concerning rolling motion into its introductory physics courses, emphasizing the importance of understanding this principle. Misapplication of this formula, or failure to account for it, often leads to significant errors in calculations involving kinetic energy and frictional forces, especially when using software like Wolfram Mathematica to simulate physical systems. Applications of this formula can be seen in the design of modern traction control systems used in automobiles, enabling enhanced stability and control.

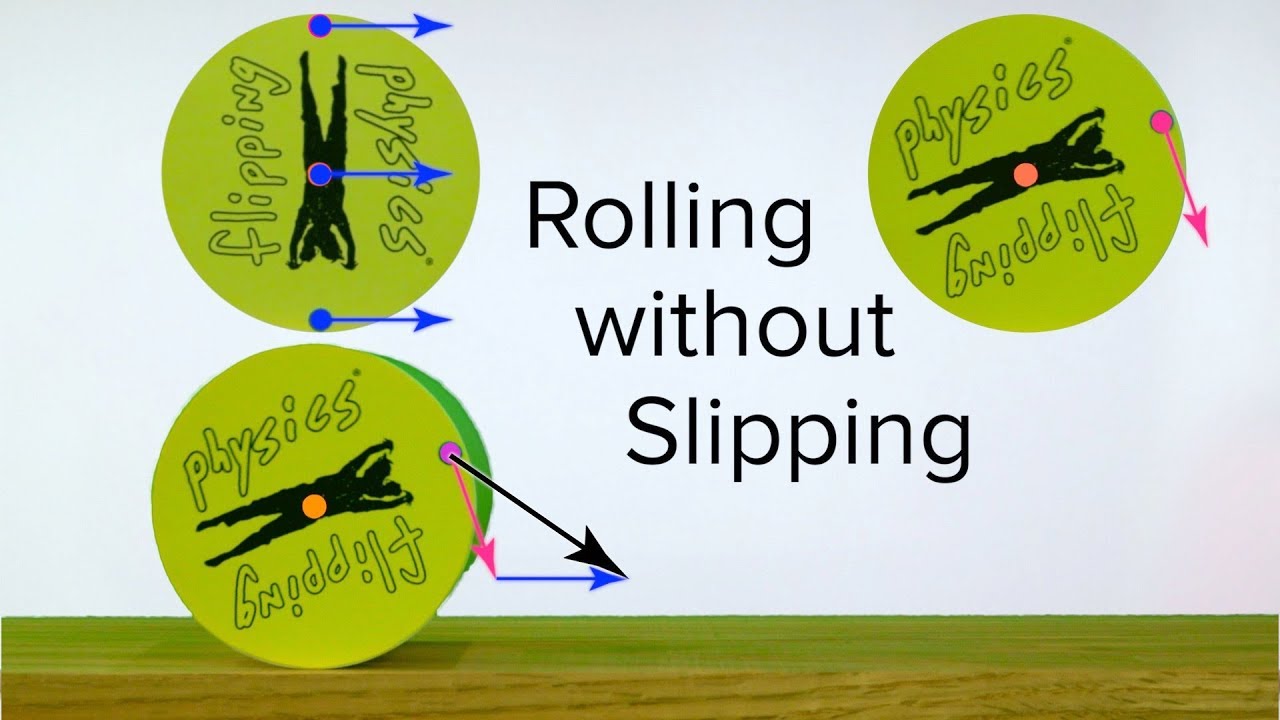
Image taken from the YouTube channel Flipping Physics , from the video titled Rolling Without Slipping Introduction and Demonstrations .

Understanding Rolling Motion: A Foundation in Physics and Engineering

Rolling motion, a ubiquitous phenomenon, represents a fundamental concept in physics and engineering. It is far more than a simple observation; it's a critical understanding of how objects interact with the world around us.

It seamlessly blends two distinct types of motion—translation and rotation—to produce a combined movement observed in everything from a car's tires to the movement of celestial bodies.

Defining Rolling Motion: Translation Meets Rotation

At its core, rolling motion is defined as the simultaneous occurrence of both translational and rotational motion of an object.

Translational motion refers to the movement of an object's center of mass from one point to another.

Rotational motion, on the other hand, involves the object's spinning or revolving around an axis.

When these two motions occur together, under specific conditions, we observe what we call rolling motion. This is most purely represented when there is rolling without slipping.

The Significance of Rolling in Scientific Disciplines

The importance of rolling motion extends deeply into both physics and engineering.

In physics, it serves as a practical model for understanding more complex mechanical systems. It elegantly demonstrates the interplay of forces, energy, and motion. It allows students and professionals to understand the behavior of objects under various conditions.

For engineers, understanding and utilizing the principles of rolling motion is crucial for designing efficient and reliable systems. Rolling elements are at the heart of countless machines and are found everywhere from vehicles to industrial equipment.

Why Rolling Matters: Practicality and Efficiency

Rolling motion is inherently linked to efficiency.

Compared to sliding friction, rolling friction is significantly lower. This allows for much less energy loss due to friction.

This makes rolling motion ideal for applications where minimizing energy expenditure is crucial. Think of wheel bearings or conveyor systems where efficient movement is necessary for the overall system to function.

Preview: Core Elements

This section provides an overview of what is required to understand the rest of this exploration of rolling motion.

• It begins with the foundational physics concepts necessary to understand rolling, like static friction, angular velocity and acceleration, linear velocity and acceleration, torque, and moment of inertia.

• Next, the explanation of the critical constraint for rolling without slipping, which relates linear and angular velocity (v = rω) is highlighted.

• Finally, the analysis of how the principles of rolling motion apply to common objects like wheels, spheres, cylinders, and discs is reviewed.

  You also like

  Cortical Laminar Necrosis Radiology: MRI Guide

These components combined will equip you with the tools to understand the fascinating dynamics of rolling motion.

Key Concepts: Foundational Principles of Rolling

To grasp the complexities of rolling motion, a firm understanding of its underlying principles is essential. Rolling motion seamlessly integrates translational and rotational dynamics, making it necessary to revisit and clarify several core physics concepts. These include static friction, angular velocity and acceleration, linear velocity and acceleration (particularly relating to the center of mass), torque, and moment of inertia. Let's delve into each concept, highlighting their individual significance and their interconnectedness in the context of rolling motion.

The Indispensable Role of Static Friction

Friction, often viewed as a hindrance, plays a crucial role in enabling rolling motion. Specifically, static friction is the force that allows an object to roll without slipping. It acts at the point of contact between the rolling object and the surface.

Unlike kinetic friction, which opposes the motion of sliding surfaces, static friction prevents any relative motion at the point of contact. Think of a tire rolling on asphalt: The portion of the tire touching the road is momentarily at rest relative to the road surface. This absence of relative motion is maintained by static friction.

If the frictional force were kinetic, the object would slide as it rotates. It's imperative to recognize that without sufficient static friction, pure rolling is impossible. Slipping would occur, transitioning the motion into a complex combination of rolling and sliding.

Angular Velocity and Acceleration: Describing Rotational Kinematics

Angular velocity (ω) and angular acceleration (α) are fundamental in describing the rotational aspects of rolling motion.

Angular velocity quantifies how quickly an object rotates, measured in radians per second (rad/s). It represents the rate of change of angular displacement.

Angular acceleration, on the other hand, describes the rate at which the angular velocity changes. Its units are radians per second squared (rad/s²). A positive angular acceleration indicates an increasing angular velocity, while a negative value signifies a decrease.

The relationship between angular velocity and acceleration is analogous to that between linear velocity and acceleration. Angular acceleration is, mathematically, the time derivative of angular velocity. If angular acceleration is constant, we can use rotational kinematic equations similar to linear motion to describe the angular motion of a rolling object.

Linear Velocity and Acceleration of the Center of Mass

While angular velocity and acceleration describe the rotation, linear velocity (v) and acceleration (a) of the center of mass describe the translational motion of the rolling object as a whole.

Linear velocity is the rate at which the center of mass changes its position, measured in meters per second (m/s). Linear acceleration is the rate of change of linear velocity, quantified in meters per second squared (m/s²).

The center of mass is a crucial concept, acting as a representative point for the entire object's motion. When analyzing the translational motion, we can treat the entire mass of the object as if it were concentrated at this single point. This significantly simplifies calculations, particularly when dealing with complex shapes or non-uniform mass distributions.

Torque: The Rotational Equivalent of Force

Torque (τ) is the rotational analogue of force. It measures the "twisting force" that causes rotation. Mathematically, it's defined as the cross product of the force vector and the displacement vector from the axis of rotation to the point where the force is applied.

The units of torque are Newton-meters (N⋅m). Torque directly influences angular acceleration. According to Newton's second law for rotation, the net torque acting on an object is equal to the product of its moment of inertia (discussed below) and its angular acceleration: τ = Iα.

Therefore, a larger torque will produce a larger angular acceleration, assuming the moment of inertia remains constant. Understanding torque is crucial for analyzing how forces cause objects to rotate, and consequently, to roll.

Moment of Inertia: Resistance to Rotational Motion

Moment of inertia (I) quantifies an object's resistance to changes in its rotational motion, akin to mass in linear motion. It depends not only on the mass of the object, but also on how that mass is distributed relative to the axis of rotation.

The farther the mass is from the axis, the greater the moment of inertia. The units of moment of inertia are kilogram-meters squared (kg⋅m²).

Different shapes have different formulas for calculating moment of inertia.

For example:

• A solid sphere of mass m and radius r has a moment of inertia of (2/5)mr².
• A solid cylinder or disc rotating about its central axis has a moment of inertia of (1/2)mr².
• A thin hoop or ring rotating about its central axis has a moment of inertia of mr².

These variations highlight the significant impact of mass distribution on an object's rotational inertia.

The moment of inertia is essential for understanding how easily (or difficult) it is to change an object's rotational speed under the influence of a torque. A higher moment of inertia requires a larger torque to achieve the same angular acceleration.

Rolling Without Slipping: The Constraint Condition

To grasp the complexities of rolling motion, a firm understanding of its underlying principles is essential. Rolling motion seamlessly integrates translational and rotational dynamics, making it necessary to revisit and clarify several core physics concepts. These include static friction, angular velocity, and the pivotal "rolling without slipping" condition. This section delves into this critical constraint, revealing its significance in simplifying the analysis of rolling motion scenarios.

The Essence of the Constraint: v = rω

The "rolling without slipping" condition is mathematically expressed as v = rω, where v represents the linear velocity of the center of mass of the rolling object, r is its radius, and ω denotes its angular velocity. This seemingly simple equation embodies a profound relationship: it dictates that the linear distance traveled by the center of the rolling object over a given time interval exactly corresponds to the arc length covered by a point on its circumference during the same interval.

This implies there is no relative motion between the point of contact of the rolling object and the surface it rolls on.

In essence, the point on the object touching the surface is momentarily at rest relative to the surface. This is only possible due to static friction, which prevents sliding.

Reducing Degrees of Freedom

The beauty of the v = rω constraint lies in its ability to reduce the number of independent variables needed to describe the motion. Without this constraint, we would have to independently track both the linear and angular motion of the object.

However, with the v = rω condition in place, only one variable is necessary.

For instance, knowing the angular velocity ω immediately allows us to determine the linear velocity v, and vice versa. This simplification is invaluable when solving problems involving rolling motion, as it reduces the complexity of the equations we need to solve.

Connecting Linear and Angular Motion: Practical Applications

The v = rω relationship is not merely a theoretical construct; it has direct implications for understanding and predicting the behavior of rolling objects. Consider a wheel rolling down a ramp: as the wheel rotates, its center of mass simultaneously accelerates linearly.

The constraint v = rω ensures that these two motions are inextricably linked.

If the wheel were to suddenly slip, this relationship would break down, and the analysis of the motion would become significantly more complicated, requiring us to account for the effects of kinetic friction.

By leveraging the v = rω condition, we can establish a direct connection between the linear and angular accelerations as well.

Differentiating the equation with respect to time, we get a = rα, where a is the linear acceleration of the center of mass and α is the angular acceleration. This equation provides a powerful tool for analyzing dynamic scenarios, such as determining the acceleration of a rolling object on an inclined plane, or calculating the final velocity of a rolling wheel after a certain distance. The constraint v = rω and its derivative are foundational to solving problems involving rolling motion, offering a simplified yet rigorous approach to understanding the interplay between linear and angular dynamics.

Application to Common Objects: Wheels, Spheres, Cylinders, and Discs

Rolling Without Slipping: The Constraint Condition

To grasp the complexities of rolling motion, a firm understanding of its underlying principles is essential. Rolling motion seamlessly integrates translational and rotational dynamics, making it necessary to revisit and clarify several core physics concepts. These include static friction, angular velocity, angular acceleration, linear velocity, linear acceleration, torque, and moment of inertia.

These foundational concepts provide the tools necessary to analyze the behavior of common objects in our daily lives, such as wheels, spheres, cylinders, and discs, all executing rolling motion.

This section will delve into how these principles are applied to these objects, providing specific examples and calculations to illustrate the theory in practice.

Wheels: The Foundation of Motion

The wheel is a ubiquitous example of rolling motion, fundamental to transportation and machinery. Its seemingly simple act of rotation embodies sophisticated physics. Understanding the dynamics of a rolling wheel involves analyzing the interplay of forces that allow it to move efficiently.

Forces Acting on a Wheel

Multiple forces govern a wheel's motion. The primary forces are:

• Applied Force: This is the force that initiates or sustains the wheel's motion. In vehicles, this comes from the engine's torque transmitted to the wheels.

• Gravitational Force: Acting downwards, this force is balanced by the normal force from the surface.

• Normal Force: The upward force exerted by the surface on the wheel, perpendicular to the contact area.

• Static Friction: Crucially, static friction at the point of contact between the wheel and the surface provides the necessary torque for rolling without slipping. It's essential to note that this is static friction, not kinetic, as the point of contact is momentarily at rest relative to the surface.

The direction of the static friction force depends on whether the wheel is accelerating or decelerating.

When a wheel is accelerating, the static friction force acts forward, providing the necessary torque to increase its angular velocity. Conversely, when decelerating, static friction acts backward, opposing the motion and reducing the angular velocity.

Understanding these forces and their interactions is vital for analyzing the dynamics of any wheeled vehicle or mechanical system.

Spheres, Cylinders, and Discs: Rolling Down Inclined Planes

A classic problem in physics involves analyzing the rolling motion of spheres, cylinders, and discs down an inclined plane. This scenario provides an excellent opportunity to apply the concepts of rolling motion and to observe how the moment of inertia affects the object's acceleration.

Analyzing Motion on an Inclined Plane

When these objects roll down an inclined plane, gravity provides the driving force. However, due to the object's moment of inertia, not all of the gravitational potential energy is converted directly into translational kinetic energy.

Some energy is converted into rotational kinetic energy, which affects the linear acceleration.

The moment of inertia, which varies for different shapes, plays a crucial role in determining the distribution of kinetic energy between translational and rotational forms.

Calculating Acceleration and Final Velocities

To determine the acceleration and final velocities of these objects, we use Newton's second law for both translation and rotation:

• ΣF = ma (sum of forces equals mass times acceleration)
• Στ = Iα (sum of torques equals moment of inertia times angular acceleration)

Combining these equations with the rolling without slipping condition (v = rω) allows us to solve for the linear acceleration (a) and angular acceleration (α).

The linear acceleration, a, is given by:

a = (g sin θ) / (1 + I / (mr²))

where:

• g is the acceleration due to gravity,
• θ is the angle of the incline,
• I is the moment of inertia,
• m is the mass,
• r is the radius of the object.

Notice how the acceleration depends on the moment of inertia. Objects with smaller I / (mr²) ratios will accelerate faster down the incline. For instance, a solid sphere (I = (2/5)mr²) will accelerate faster than a hollow sphere (I = (2/3)mr²), assuming they have the same mass and radius.

Once the acceleration is known, kinematic equations can be used to determine the final velocity at the bottom of the incline. By varying the shape of the rolling object, it becomes very clear how an object's moment of inertia dictates its ability to resist angular acceleration, dictating its overall linear velocity.

Analyzing Rolling Motion: Free Body Diagrams and Equations of Motion

Application to Common Objects: Wheels, Spheres, Cylinders, and Discs Rolling Without Slipping: The Constraint Condition

To grasp the complexities of rolling motion, a firm understanding of its underlying principles is essential. Rolling motion seamlessly integrates translational and rotational dynamics, making it necessary to revisit and clarify several key concepts. This requires a meticulous approach, often beginning with the construction of free body diagrams to accurately represent the forces at play and subsequently formulating equations of motion based on Newton’s laws.

The Indispensable Free Body Diagram

The cornerstone of any rigorous analysis in mechanics, and especially within the context of rolling motion, is the free body diagram (FBD). A well-constructed FBD serves as a visual representation of all external forces acting on the object of interest, thereby simplifying the process of applying Newton’s laws. Without an accurate FBD, the subsequent mathematical analysis is prone to error and misinterpretation.

Identifying Forces in Rolling Motion

When dealing with rolling objects, several forces are typically present:

• Gravitational Force (Weight): Acting vertically downwards through the center of mass. This force is fundamental and must always be included.

• Normal Force: Exerted by the surface on the object, acting perpendicular to the contact surface. Its magnitude depends on the specific scenario and other forces acting on the object.

• Friction Force: The tangential force acting at the point of contact between the rolling object and the surface. In the case of rolling without slipping, this is static friction, which prevents relative motion between the contact points. It's direction opposes the tendency to slide.

The accurate determination of the direction and point of application of each force is critical for the subsequent formulation of equations of motion.

Equations of Motion: Bridging Forces and Motion

With the FBD in place, the next step involves applying Newton’s second law, both for translational motion (F = ma) and rotational motion (τ = Iα). This application allows us to relate the forces acting on the object to its linear and angular accelerations.

Newton's Second Law for Translation

This law states that the net force acting on an object is equal to the product of its mass and its acceleration. In the context of rolling motion, this equation is applied to the center of mass of the rolling object:

∑F = ma

where ∑F represents the vector sum of all external forces acting on the object, m is the mass of the object, and a is the linear acceleration of its center of mass.

Newton's Second Law for Rotation

This law states that the net torque acting on an object is equal to the product of its moment of inertia and its angular acceleration. This equation describes the rotational dynamics of the rolling object:

∑τ = Iα

where ∑τ is the net torque acting on the object, I is the moment of inertia of the object about its axis of rotation (usually through the center of mass), and α is its angular acceleration.

Incorporating the Rolling Without Slipping Constraint

A key aspect of analyzing rolling motion is the condition that the object rolls without slipping. This constraint establishes a direct relationship between the linear velocity (v) and angular velocity (ω) of the object, given by:

v = rω

where r is the radius of the rolling object. Differentiating this equation with respect to time yields a relationship between the linear acceleration (a) and angular acceleration (α):

a = rα

This constraint is crucial because it reduces the number of independent variables in the problem, allowing us to solve for unknowns more easily. This kinematic constraint ties together translational and rotational movement.

Solving for Unknown Variables

By combining the equations of motion (Newton’s second law for translation and rotation) with the rolling without slipping constraint, one can solve for unknown variables such as the linear acceleration, angular acceleration, and the static friction force.

This generally involves solving a system of simultaneous equations. The systematic application of these principles ensures a thorough and accurate analysis of rolling motion problems.

Analyzing Rolling Motion: Free Body Diagrams and Equations of Motion Application to Common Objects: Wheels, Spheres, Cylinders, and Discs Rolling Without Slipping: The Constraint Condition

To grasp the complexities of rolling motion, a firm understanding of its underlying principles is essential. Rolling motion seamlessly integrates translational and rotational dynamics, and the concept of the center of mass emerges as a pivotal tool in simplifying its analysis. By understanding its role, we can develop a greater understanding of the interplay between the different aspects of motion.

The Role of the Center of Mass in Rolling Motion

The center of mass (COM) is the unique point where the weighted relative position of the distributed mass sums to zero. It is, in essence, the average position of all the mass in the system. Its significance in mechanics cannot be overstated, particularly when dealing with complex motion like rolling.

Simplifying Analysis Through a Central Reference Point

The center of mass allows us to reduce the complexity of extended objects into a single, representative point. This simplification is critical in rolling motion because it enables us to decouple the translational and rotational aspects of movement. By treating the object's entire mass as if it were concentrated at the COM, we can apply Newton's laws of motion directly to this point.

This reduces a complex system to a more manageable one.

The translational motion of the object then becomes the motion of its COM, which greatly simplifies calculations and provides insights into the object’s overall trajectory.

Treating the Object's Mass as Concentrated at the Center of Mass

When analyzing rolling motion, we can consider all external forces as acting on the center of mass. This allows us to calculate the net force and, consequently, the linear acceleration of the object using F = ma, where F is the net force, m is the total mass, and a is the acceleration of the COM.

Moreover, the torque due to these forces can be calculated about the center of mass, enabling us to determine the angular acceleration using τ = Iα, where τ is the net torque, I is the moment of inertia about the COM, and α is the angular acceleration.

This approach is particularly useful when dealing with objects of irregular shapes or non-uniform mass distributions.

Decoupling Translational and Rotational Motion

One of the most powerful aspects of using the center of mass is its ability to decouple the translational and rotational motion. This decoupling allows us to analyze each aspect independently, and then relate them through the constraint condition for rolling without slipping (v = rω).

For example, consider a sphere rolling down an inclined plane. The gravitational force acts on the COM, causing it to accelerate downwards. At the same time, the torque due to the frictional force (acting at the point of contact) causes the sphere to rotate. By analyzing these motions separately, we can determine the sphere's linear and angular acceleration, and hence, its overall motion.

Practical Implications

The concept of the center of mass is not just a theoretical construct; it has profound practical implications. In engineering, understanding the COM is crucial for designing stable structures, efficient machines, and safe vehicles. For instance, the placement of the COM in a car affects its stability and handling, while in robotic design, precise control of the COM is essential for balance and maneuverability.

In conclusion, the center of mass is a cornerstone concept in understanding and analyzing rolling motion.

By treating an object's mass as concentrated at a single point, we can simplify calculations, decouple translational and rotational motions, and gain valuable insights into the object's overall dynamics.

This approach is essential for both theoretical analysis and practical applications, making the center of mass an indispensable tool for anyone studying or working with mechanics.

Real-World Applications of Rolling Motion

Analyzing Rolling Motion: Free Body Diagrams and Equations of Motion Application to Common Objects: Wheels, Spheres, Cylinders, and Discs Rolling Without Slipping: The Constraint Condition

To grasp the complexities of rolling motion, a firm understanding of its underlying principles is essential. Rolling motion seamlessly integrates translational and rotational dynamics, impacting diverse engineering domains and influencing the design and functionality of countless machines and vehicles we encounter daily. Understanding these real-world impacts illustrates the practical significance of grasping this combined motion.

Rolling Motion in Engineering Mechanics

Rolling motion isn’t merely a theoretical concept confined to textbooks. It’s a foundational principle underpinning numerous engineering applications, particularly within machine and vehicle design. A thorough comprehension of rolling dynamics directly translates into more efficient, safer, and reliable systems.

Machine Design: Gears and Pulleys

In machine design, elements such as gears and pulleys critically rely on the principles of rolling motion. Gears, with their precisely designed teeth, transmit rotational motion and torque from one shaft to another, efficiently altering speed and force.

Pulleys, likewise, utilize rolling contact between a belt or rope and a wheel to facilitate the lifting of loads or the transmission of power across distances. The efficient functioning of these mechanisms hinges on minimizing slippage and maximizing the transfer of energy, a direct result of understanding and applying rolling motion principles.

Vehicle Design: Tires and Transmissions

The same tenets are at play in vehicle engineering. Tires, the primary interface between a vehicle and the road, rely on static friction to facilitate rolling without slipping. The design of tire treads and the selection of rubber compounds are crucial for optimizing grip and ensuring safe and controlled motion.

Transmissions, intricate systems of gears and shafts, are engineered to efficiently transfer power from the engine to the wheels, optimizing torque and speed for varying driving conditions. Understanding rolling motion is paramount in minimizing energy loss, reducing wear, and maximizing vehicle performance.

Real-World Examples: Efficiency and Safety

The practical implications of understanding rolling motion manifest in numerous real-world examples. Consider the design of high-efficiency transmissions in hybrid vehicles. By optimizing gear ratios and minimizing frictional losses, engineers can significantly improve fuel economy and reduce emissions. This requires a deep understanding of the dynamics of rolling and rotation.

Similarly, the development of advanced braking systems, such as anti-lock braking systems (ABS), relies on precise control of wheel rotation to prevent skidding and maintain directional stability. These systems intelligently modulate brake pressure to ensure that the wheels continue to roll without locking up, thereby maximizing braking force and driver control.

Another compelling example is the design of roller bearings in industrial machinery. These bearings minimize friction and wear by replacing sliding contact with rolling contact, enabling smoother operation, reduced energy consumption, and extended equipment lifespan.

The design of bicycle wheels, optimizing for both speed and load-bearing capabilities, requires understanding the interplay of rotational inertia, rolling resistance, and the distribution of mass.

Each of these instances underscores the undeniable significance of rolling motion in engineering practice, highlighting its transformative impact on efficiency, safety, and overall system performance. The principles of rolling motion also provide a framework for diagnosing potential issues in existing systems, as well as for innovating novel solutions to complex mechanical problems.

Rolling Motion in Education: Teaching and Learning

To grasp the complexities of rolling motion, a firm understanding of its underlying principles is essential. Rolling motion, a fundamental concept in introductory mechanics, often presents unique pedagogical challenges. This section will discuss the common approaches to teaching rolling motion, prevalent student misconceptions, and effective teaching strategies.

Standard Pedagogical Approaches

In most introductory physics courses, rolling motion is typically introduced after students have a solid foundation in translational and rotational kinematics and dynamics. The topic is commonly approached by building upon previously learned concepts, such as Newton's laws and energy conservation principles.

The curriculum usually starts by defining rolling motion as a combination of translational and rotational motion.

The condition for rolling without slipping (v = rω) is then introduced as a crucial constraint. This is often followed by analyzing the forces and torques involved in rolling motion using free-body diagrams and Newton's second law for both translation and rotation.

Common Student Difficulties and Misconceptions

Rolling motion is a topic rife with potential for student misunderstanding. One common difficulty lies in the simultaneous consideration of both translational and rotational motion. Students often struggle to integrate these two aspects, leading to confusion in problem-solving.

Another prevalent misconception involves the role of static friction in rolling motion. Students often incorrectly assume that friction always opposes motion and dissipates energy. They fail to recognize that static friction is essential for providing the torque necessary to initiate and sustain rolling without slipping.

Furthermore, the concept of the moment of inertia can be challenging for students. Understanding how mass distribution affects an object's resistance to rotational acceleration requires a solid grasp of calculus and spatial reasoning, which some students may lack.

Effective Teaching Strategies

To address these challenges, instructors can employ several effective teaching strategies.

Emphasize Visual Aids

Visual aids, such as diagrams and animations, can be invaluable in illustrating the combined translational and rotational aspects of rolling motion. Demonstrations involving rolling objects on inclined planes or other surfaces can also enhance student understanding by providing concrete examples.

Interactive Simulations

The use of interactive simulations can allow students to explore the effects of varying parameters, such as friction coefficients or moments of inertia, on rolling motion. By manipulating these variables and observing the resulting changes in motion, students can develop a more intuitive understanding of the underlying principles.

Problem-Solving Practice

Providing ample opportunities for problem-solving is crucial for reinforcing student learning. Problems should range in difficulty, starting with simpler scenarios and gradually progressing to more complex situations involving multiple forces and constraints.

Emphasize the importance of drawing accurate free-body diagrams and applying Newton's laws systematically. Encourage students to break down complex problems into smaller, more manageable steps to minimize errors.

Conceptual Questioning

Conceptual questions can be used to probe student understanding and identify any remaining misconceptions. These questions should focus on the underlying principles of rolling motion rather than rote memorization of formulas. For example: "Why does a solid sphere roll down an incline faster than a hollow sphere of the same mass and radius?"

By focusing on both conceptual understanding and problem-solving skills, instructors can help students develop a deeper and more meaningful understanding of rolling motion. This prepares them for more advanced topics in mechanics and engineering.

Video: Rolling Without Slipping Formula: A Practical Guide

Play Video

So, there you have it! Hopefully, this guide has demystified the rolling without slipping formula and given you the tools to tackle those physics problems with confidence. Now go forth and conquer those rotational motion challenges!