Reduced Mass: Calculation, Applications & Guide
In the realm of classical mechanics, the reduced mass, a concept pioneered by figures like Sir Isaac Newton, simplifies the analysis of two-body problems by effectively transforming them into a single-body problem. This transformation is particularly useful when examining systems such as diatomic molecules, where the vibrational and rotational behaviors are key to understanding their spectroscopic properties. The calculation of reduced mass, represented as μ = (m1 * m2) / (m1 + m2), allows researchers at institutions like the Massachusetts Institute of Technology (MIT) to model complex interactions, offering insights that would otherwise be obscured by the complexities of dealing with two independent masses. Moreover, software tools like Mathematica utilize the reduced mass concept to simulate molecular dynamics, facilitating advancements in fields ranging from material science to chemical kinetics.
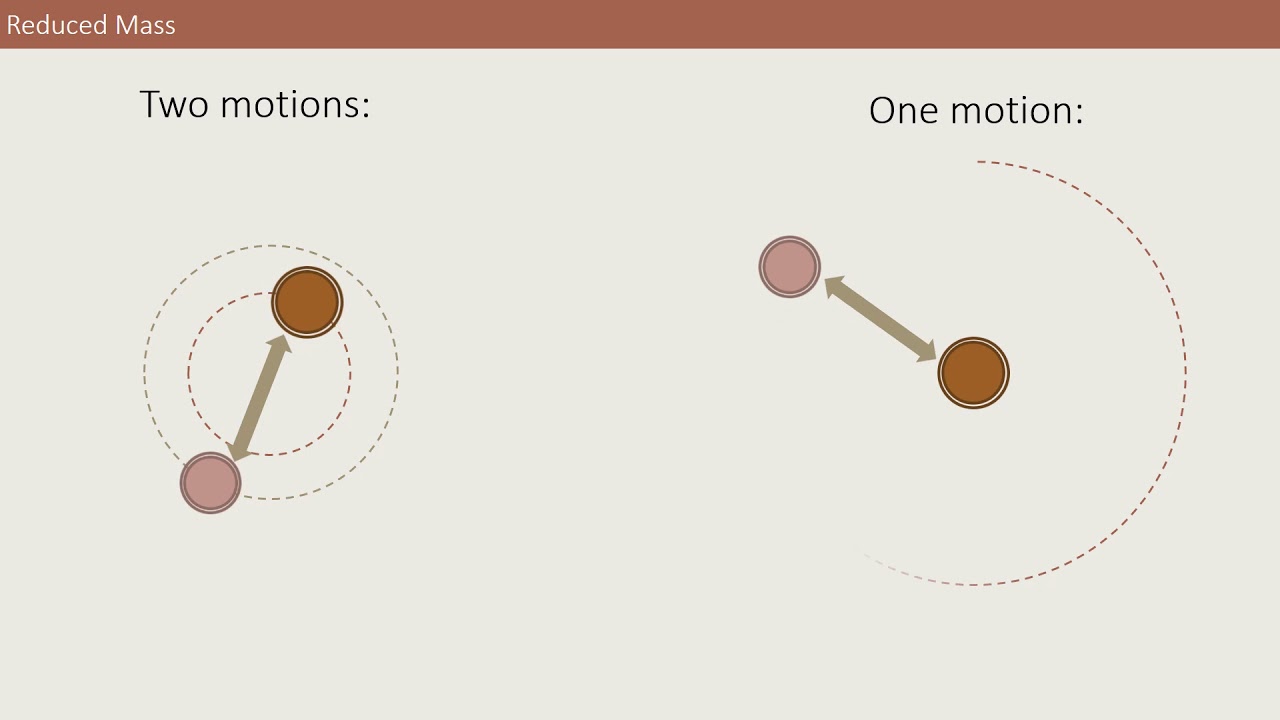
Image taken from the YouTube channel Chris Armstrong , from the video titled Reduced mass visualisation .
Unveiling the Power of Reduced Mass: Simplifying Two-Body Dynamics
The concept of reduced mass stands as a cornerstone in simplifying the complexities inherent in two-body problems across diverse scientific domains. From the intricacies of molecular vibrations to the grand scale of celestial mechanics, reduced mass provides a powerful lens through which we can transform seemingly intractable calculations into manageable and insightful analyses.
At its core, reduced mass serves as an effective mass that encapsulates the combined inertial properties of two interacting bodies. By shifting the perspective from two individual entities to a single, effective mass, we gain the ability to analyze the relative motion of the system with remarkable ease.
Defining Reduced Mass: An Effective Mass for Two-Body Systems
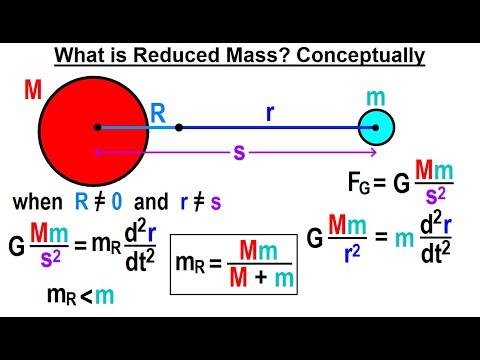
Reduced mass, denoted by the Greek letter μ (mu), represents the effective inertial mass of a system comprising two bodies. It's particularly valuable when analyzing the relative motion of two objects bound by a force that depends only on the distance between them.
This concept allows us to treat the two-body problem as if it were a single body orbiting a fixed point, significantly simplifying the mathematical formulation and subsequent analysis.
The Mathematical Formulation: A Concise Expression
The reduced mass (μ) is mathematically defined as:
μ = (m₁ * m₂) / (m₁ + m₂)
where m₁ and m₂ represent the masses of the two interacting bodies.
This simple equation elegantly captures the combined inertial effect of the two bodies, allowing us to replace them with a single, effective mass for calculations involving their relative motion.
Significance: Transforming Two Bodies into One
The true power of reduced mass lies in its ability to transform a complex two-body problem into an equivalent one-body problem. This transformation is achieved by shifting to a center-of-mass frame of reference, where the motion of the two bodies is described relative to their common center of mass.
In this frame, the problem is reduced to analyzing the motion of a single particle with a mass equal to the reduced mass, acted upon by a force derived from the original interaction between the two bodies. This simplification drastically reduces the complexity of the mathematical treatment, making the problem tractable.
Broad Applications Across Disciplines
The concept of reduced mass finds widespread application in both physics and chemistry:
-
In molecular vibrations, it allows us to calculate the vibrational frequencies of diatomic molecules and analyze their infrared spectra.
-
In celestial mechanics, it simplifies the analysis of binary star systems and planet-star interactions.
-
In atomic physics, it’s used to describe the energy levels of hydrogen-like atoms.
Scope: Theoretical Foundations, Practical Applications, and Computational Tools
Our exploration of reduced mass will delve into the theoretical foundations underpinning its use, demonstrating how it arises from classical and quantum mechanical considerations.
We will then explore its practical applications across diverse fields, illustrating its power in solving real-world problems.
Finally, we will introduce the computational tools available for calculating reduced mass and applying it to complex systems, empowering you to harness its potential in your own research and studies.
Theoretical Foundation: From Two Bodies to One
Unveiling the Power of Reduced Mass: Simplifying Two-Body Dynamics The concept of reduced mass stands as a cornerstone in simplifying the complexities inherent in two-body problems across diverse scientific domains. From the intricacies of molecular vibrations to the grand scale of celestial mechanics, reduced mass provides a powerful lens through which we can transform seemingly intractable scenarios into manageable, solvable models. In this section, we delve into the theoretical underpinnings of this transformative tool, elucidating its role in both classical and quantum mechanical frameworks.
The Intricacies of the Classical Two-Body Problem
The classical two-body problem, at its core, involves analyzing the motion of two objects interacting via a mutual force, typically gravity or electrostatics. While seemingly simple, a direct solution becomes complicated due to the coupled nature of their motion. Each body's movement influences, and is influenced by, the other, creating a system of interdependent equations.
The complexity arises from the need to track the individual positions and velocities of both objects simultaneously, accounting for their continuous interaction. This intricate dance makes finding a general analytical solution a formidable task.
Transforming to a One-Body Problem with Reduced Mass
The brilliance of the reduced mass concept lies in its ability to convert this two-body problem into an equivalent one-body problem. This transformation simplifies the mathematical description by effectively reducing the system to a single "effective" particle with a specific mass, the reduced mass (μ), moving under the influence of a modified potential.
By introducing the reduced mass, we can describe the relative motion of the two bodies as if a single particle were orbiting a fixed point. This simplification dramatically reduces the mathematical complexity, making the problem tractable.
The Role of the Center of Mass
The center of mass (COM) plays a crucial role in this transformation. It represents the average position of all the mass in the system, weighted by their respective masses.
In a two-body system, the COM is a point that lies on the line connecting the two bodies, closer to the more massive object. The significance of the COM is that, in the absence of external forces, it moves with constant velocity, simplifying the overall analysis.
The Center of Mass Frame: A Simplified Perspective
Analyzing the system from the center of mass frame – a coordinate system where the COM is at rest – provides a powerful simplification. In this frame, the total momentum of the system is zero, and the motion of the two bodies can be described relative to the COM.
This allows us to focus on the relative motion between the two bodies, which is precisely what the reduced mass formulation captures.
Reduced Mass in Classical Mechanics
In classical mechanics, the reduced mass (μ) significantly simplifies the expressions for kinetic and potential energy.
The kinetic energy of the system can be expressed in terms of the reduced mass and the relative velocity between the two bodies. Similarly, the potential energy depends only on the relative distance between the two bodies, allowing for a straightforward treatment of their interaction.
Using reduced mass, the Lagrangian and Hamiltonian formulations of the problem become much simpler. This provides a direct and efficient way to analyze the dynamics of the system.
Quantum Mechanical Applications
The application of reduced mass extends seamlessly into quantum mechanics, especially when dealing with atomic and molecular systems. For instance, when solving the Schrödinger equation for the hydrogen atom, the reduced mass of the electron-proton system is used instead of the electron's mass alone.
This correction, although small, leads to more accurate predictions of atomic energy levels. In molecules, reduced mass is crucial for calculating vibrational frequencies and rotational energy levels, providing insights into molecular structure and dynamics.
The use of reduced mass allows us to accurately model the behavior of diatomic molecules, providing crucial insights into their spectra and behavior. The concept also applies to exciton dynamics in solid-state physics.
Reduced Mass in Spectroscopy: Decoding Molecular Secrets
The concept of reduced mass stands as a cornerstone in simplifying the complexities inherent in two-body problems across diverse scientific domains. From the intricacies of molecular vibrations to the grand scale of celestial mechanics, its utility is undeniable. Now, we delve specifically into its pivotal role within spectroscopy, focusing on how reduced mass unlocks the secrets encoded in molecular spectra.
Vibrational Spectroscopy: Unveiling Molecular Motion
Vibrational spectroscopy provides a window into the dynamic world of molecular vibrations. Molecules aren't static structures, but rather systems of atoms constantly in motion. The vibrational frequencies of these motions are directly related to the masses of the atoms involved and the strength of the chemical bonds between them.
The reduced mass plays a crucial role in quantifying these vibrations. By simplifying the two-body vibrational problem into an equivalent one-body problem, it allows for easier calculation of vibrational frequencies. This simplification is essential for interpreting vibrational spectra and extracting information about molecular structure and bonding.
Hooke's Law and Diatomic Molecules
A fundamental illustration of this principle is the application of Hooke's Law to diatomic molecules. Hooke's Law, which describes the force required to stretch or compress a spring, can be adapted to model the vibrational motion of a diatomic molecule.
The equation derived from Hooke's Law allows us to calculate the vibrational frequency (ν) of the molecule:
ν = (1 / 2π)
**√(k / μ)
Where k is the force constant representing the bond strength, and μ is the reduced mass. This equation highlights the inverse relationship between reduced mass and vibrational frequency: heavier molecules or molecules with heavier atoms will vibrate at lower frequencies.
Therefore, the vibrational frequencies, readily observable using techniques such as infrared (IR) spectroscopy, directly inform us of bond strengths and atomic masses within the molecule. Any changes in these measurable values would alter the overall calculation of the reduced mass.
Rotational Spectroscopy: Probing Molecular Structure
Beyond vibrations, molecules also exhibit rotational motion. Rotational spectroscopy explores these motions, revealing valuable information about molecular geometry and bond lengths. The reduced mass appears again, this time in the calculation of the moment of inertia.
Moment of Inertia and Rotational Energy Levels
The moment of inertia (I) is a measure of a molecule's resistance to changes in its rotational motion. For a diatomic molecule, the moment of inertia is given by:
I = μ** r²
Where μ is the reduced mass, and r is the bond length.
The moment of inertia directly influences the rotational energy levels of the molecule. These energy levels are quantized, meaning that a molecule can only rotate at specific, discrete energy values. The energy levels are given by:
E = (ħ² / 2I) * J(J+1)
Where ħ is the reduced Planck constant, and J is the rotational quantum number.
The spacing between these rotational energy levels is inversely proportional to the moment of inertia, and therefore inversely proportional to the reduced mass if bond length is held constant.
Analyzing Molecular Rotational Spectra
Rotational spectroscopy measures the absorption or emission of electromagnetic radiation as a molecule transitions between rotational energy levels. The resulting spectrum consists of a series of lines, each corresponding to a specific rotational transition.
By analyzing the spacing between these lines, we can determine the moment of inertia of the molecule, and subsequently, the bond length if the reduced mass is known, or vice versa. This technique provides a precise and powerful method for determining molecular structure.
The astute application of reduced mass enables scientists to interpret complex spectra and accurately determine vital molecular properties. Consequently, the accurate computation of reduced mass leads to the precise evaluation of a compound's properties in both vibrational and rotational contexts.
Applications in Physics: From Stars to Particles
The concept of reduced mass stands as a cornerstone in simplifying the complexities inherent in two-body problems across diverse scientific domains. From the intricacies of molecular vibrations to the grand scale of celestial mechanics, its utility is undeniable. Now, we delve specifically into its profound applications within the broader field of physics, spanning the cosmos with astrophysics to the subatomic realm with particle physics.
Reduced Mass in Celestial Mechanics and Astrophysics
Celestial mechanics, concerned with the motion of celestial objects, often grapples with the gravitational interactions between two massive bodies. A typical case includes binary star systems and planet-star interactions.
The direct solution of the two-body problem is complex; however, through the strategic implementation of reduced mass, the intricate dance of two celestial bodies can be elegantly transformed into a simpler, equivalent one-body problem. This simplified framework allows for easier computation of orbital parameters.
Analyzing Binary Star Systems
Consider a binary star system, where two stars orbit around their common center of mass. Instead of separately analyzing the motion of each star relative to an external point, we can use the reduced mass μ to describe the motion of a fictitious body with mass μ orbiting a fixed point located at the center of mass.
This approach drastically reduces the mathematical complexity, enabling accurate predictions of orbital periods, shapes, and stability.
Planet-Star Interactions
Similarly, when analyzing the motion of a planet around a star, the reduced mass concept accounts for the fact that both the planet and the star revolve around their common center of mass. While the star's movement might be subtle due to its significantly larger mass, the reduced mass elegantly incorporates this effect, offering a more precise description of the planet's orbit.
This is particularly relevant in exoplanet research, where detecting the subtle "wobble" of a star due to an orbiting planet is a key method of discovery. The more accurate the calculations (through reduced mass), the higher the likelihood of discovering planets.
Reduced Mass in Particle Physics
The reach of reduced mass extends far beyond celestial bodies, finding significant applications in the quantum world of particle physics. In this domain, understanding the interactions between two particles is crucial.
Analyzing Two-Particle Interactions
When studying collisions or bound states of two particles (e.g., an electron and a positron forming positronium), the reduced mass formalism again offers a simplifying lens. It allows us to treat the system as a single particle with mass μ moving under the influence of a central potential.
This simplification is invaluable in calculating energy levels, wave functions, and other crucial properties of the system.
Calculating Scattering Cross-Sections
Another vital application arises in the calculation of scattering cross-sections. In scattering experiments, particles are fired at each other, and the probability of them scattering in a particular direction is quantified by the scattering cross-section. The reduced mass plays a key role in accurately determining these cross-sections, particularly when dealing with non-negligible masses for both interacting particles.
By incorporating the reduced mass, theoretical models can more accurately predict experimental outcomes, furthering our understanding of fundamental particle interactions. The precision enabled by this seemingly simple adjustment is vital in the relentless pursuit of uncovering the deepest secrets of our universe.
Computational Tools: Calculating Reduced Mass
[Applications in Physics: From Stars to Particles
The concept of reduced mass stands as a cornerstone in simplifying the complexities inherent in two-body problems across diverse scientific domains. From the intricacies of molecular vibrations to the grand scale of celestial mechanics, its utility is undeniable. Now, we delve specifically into its practical calculation, exploring the array of computational tools available to researchers and students alike.]
The accurate calculation of reduced mass is essential for quantitative analysis in physics and chemistry. Fortunately, a variety of tools exist, ranging from simple formula application to sophisticated software simulations, making this calculation accessible and precise.
Deriving the Reduced Mass Formula: A Foundational Approach
The reduced mass formula, μ = (m₁ * m₂) / (m₁ + m₂), provides a concise method to represent the effective mass of a two-body system. The formula is derived from considering the kinetic energy of two bodies rotating about their center of mass.
This equation emerges from the transformation of a two-body problem into an equivalent one-body problem, enabling easier analysis of relative motion. Understanding this derivation is crucial for grasping the physical meaning of reduced mass.
Detailed Breakdown of the Formula
Let's break down the formula for better understanding:
- μ represents the reduced mass.
- m₁ and m₂ are the masses of the two bodies in question.
The formula effectively replaces the two individual masses with a single, effective mass that captures the dynamics of their relative motion. It is important to note that the reduced mass is always less than or equal to the smaller of the two masses.
Practical Examples: Applying the Formula
To illustrate the utility of the formula, consider a few practical examples:
-
Hydrogen Atom: In a hydrogen atom, where m₁ is the mass of the proton and m₂ is the mass of the electron, the reduced mass is very close to the mass of the electron due to the proton's significantly larger mass.
-
Diatomic Molecule (e.g., CO): In carbon monoxide, where m₁ is the mass of carbon and m₂ is the mass of oxygen, the reduced mass is used to calculate the vibrational frequency of the molecule.
By plugging in the respective masses, one can compute the reduced mass and utilize it to predict various properties of the system. These properties can be such as bond strength, atomic spacing, vibrational frequencies, and rotational inertia.
Online Calculators: Quick and Convenient Computation
Numerous online reduced mass calculators are readily available, offering a quick and convenient method for computation. These calculators require only the input of the two masses, and they instantly provide the reduced mass value.
These tools are particularly useful for quick checks, educational purposes, or when computational resources are limited. Their accessibility promotes wider adoption of reduced mass calculations in various applications.
Mathematical Software: Solving Complex Problems
More complex scenarios, particularly those involving differential equations or simulations, often require advanced mathematical software like Mathematica, MATLAB, or Python. These tools enable users to solve equations incorporating reduced mass within larger models.
These advanced software tools are vital for simulating complex systems, such as molecular dynamics simulations or celestial mechanics calculations, providing insights beyond simple analytical solutions. The tools enable more advanced simulations and modeling.
Advanced Simulations and Modeling
Advanced simulations leverage reduced mass to streamline calculations and improve computational efficiency. Molecular dynamics simulations, for instance, often use reduced mass to model the vibrational modes of molecules, significantly reducing the computational load compared to treating each atom individually.
Similarly, in astrophysical simulations, the interaction between stars or planets can be simplified using reduced mass, allowing for more extended simulations and more accurate predictions. This advanced modeling brings computational efficiency and provides deeper insights.
The concept of reduced mass stands as a cornerstone in simplifying the complexities inherent in two-body problems across diverse scientific domains. From the intricacies of molecular vibrations to the grand scale of celestial mechanics, its utility is undeniable.
However, its true power is only fully realized when considering its implications within the broader energetic landscape of a system. Delving deeper into these advanced concepts reveals a more nuanced understanding of how reduced mass influences kinetic and potential energies, ultimately dictating the behavior of physical systems.
Advanced Concepts: Kinetic and Potential Energy Landscapes
Beyond its basic definition as a mere simplification tool, the reduced mass profoundly impacts the energetic properties of two-body systems. Understanding this connection is crucial for advanced analyses and predictive modeling.
Reduced Mass and Kinetic Energy
The kinetic energy of a two-body system is intimately linked to the reduced mass.
The reduced mass provides an elegant way to describe the kinetic energy associated with the relative motion of the two bodies.
Instead of dealing with individual kinetic energies and velocities, we can express the total kinetic energy due to relative motion in terms of the reduced mass and the relative velocity.
This simplification streamlines calculations and offers a clearer picture of the system's dynamics.
The formula for kinetic energy in terms of reduced mass (( \mu )) and relative velocity (( v )) is:
(KE = \frac{1}{2} \mu v^2)
This equation neatly encapsulates the kinetic energy associated with the relative movement of the two bodies, making it far easier to analyze than dealing with individual kinetic energies.
The Interplay with Potential Energy
The potential energy function, describing the interaction between the two bodies, works in tandem with the reduced mass to govern the system's overall dynamics.
The potential energy dictates the forces acting on the bodies.
The reduced mass determines how they respond to these forces.
Different potential energy functions lead to diverse behaviors, ranging from simple harmonic oscillations to complex orbital trajectories.
Examples of such systems include:
-
Harmonic Oscillator: ( V(r) = \frac{1}{2} k r^2 )
-
Gravitational Potential: ( V(r) = -\frac{G m1 m2}{r} )
-
Coulomb Potential: ( V(r) = \frac{q1 q2}{4 \pi \epsilon_0 r} )
Effective Potential: A Simplified Perspective
The concept of effective potential arises when dealing with systems exhibiting rotational or angular motion.
It combines the actual potential energy with a centrifugal potential term.
This centrifugal term accounts for the kinetic energy associated with the angular motion, effectively modifying the potential landscape.
The effective potential simplifies the analysis of orbital motion by reducing the problem to a one-dimensional system.
For example, in analyzing planetary motion, the effective potential allows us to determine stable orbits and understand the conditions for escape or collision.
By analyzing the shape of the effective potential, we can predict the system's behavior.
- Stable orbits correspond to minima in the effective potential.
- Unstable orbits or scattering events can also be predicted.
The reduced mass plays a crucial role in defining the centrifugal potential term.
It directly influences the shape and characteristics of the effective potential. This highlights the profound impact of reduced mass on the dynamics of systems with angular motion.
Molecular Physics and Chemistry: A Deeper Dive
[The concept of reduced mass stands as a cornerstone in simplifying the complexities inherent in two-body problems across diverse scientific domains. From the intricacies of molecular vibrations to the grand scale of celestial mechanics, its utility is undeniable. However, its true power is only fully realized when considering its implications within the more specialized fields of...] molecular physics and chemistry, where it serves as an indispensable tool for deciphering the secrets encoded in molecular spectra and understanding the fundamental properties of chemical bonds.
This section delves into the nuanced applications of reduced mass within these disciplines, exploring how it enables us to quantitatively link molecular structure to observable spectroscopic phenomena.
Calculating Vibrational Frequencies
The vibrational frequency of a diatomic molecule is directly related to the strength of the chemical bond connecting the two atoms and the masses of the atoms themselves.
The reduced mass, μ, elegantly encapsulates the mass dependence.
In the simple harmonic oscillator approximation, the vibrational frequency (ν) is given by:
ν = (1 / 2π) * √(k / μ)
where k is the force constant, representing the bond strength.
A larger force constant (stronger bond) results in a higher vibrational frequency, while a larger reduced mass leads to a lower frequency.
Isotopic substitution, for example, provides a direct experimental test of this relationship.
Replacing a lighter atom with a heavier isotope increases the reduced mass, predictably shifting the vibrational frequency to lower values.
This isotopic effect is routinely used to confirm vibrational mode assignments and to refine our understanding of molecular potential energy surfaces.
Determining Rotational Frequencies
The rotational energy levels of a molecule are quantized, and the frequencies of transitions between these levels fall into the microwave region of the electromagnetic spectrum.
The moment of inertia (I) of a diatomic molecule is central to understanding its rotational behavior and is defined as:
I = μr²
where r is the bond length.
The rotational constant (B), which determines the spacing between rotational energy levels, is inversely proportional to the moment of inertia:
B = h / (8π²cI)
where h is Planck's constant and c is the speed of light.
Therefore, the reduced mass plays a crucial role in determining the rotational spectrum.
Heavier molecules (larger reduced mass) have smaller rotational constants and more closely spaced rotational energy levels.
Precise measurements of rotational spectra, combined with accurate knowledge of atomic masses, can yield highly accurate bond lengths.
Analyzing Molecular Spectra and Bond Characteristics
Spectroscopic techniques, such as infrared (IR) and microwave spectroscopy, provide a wealth of information about molecular structure and dynamics.
By analyzing the vibrational and rotational spectra of molecules, and by carefully considering the role of reduced mass, we can infer important properties such as bond strengths, bond lengths, and molecular geometries.
For example, the presence of specific functional groups in a molecule can be identified by their characteristic vibrational frequencies in the IR spectrum.
The exact position of these frequencies is sensitive to the reduced masses of the atoms involved in the vibration, allowing for the differentiation of isotopologues and the analysis of complex mixtures.
Furthermore, deviations from the simple harmonic oscillator model can be explored by examining the anharmonicity of vibrational modes, providing insights into the shape of the molecular potential energy surface and the possibility of bond dissociation.
In summary, reduced mass serves as a vital bridge connecting the microscopic world of atoms and bonds to the macroscopic world of observable spectra.
Its application in molecular physics and chemistry allows us to extract precise and meaningful information about the structure and dynamics of molecules, advancing our understanding of the fundamental principles that govern the behavior of matter.
Video: Reduced Mass: Calculation, Applications & Guide
FAQs: Reduced Mass
What's the basic formula for calculating reduced mass, and when is it used?
Reduced mass (μ) is calculated as μ = (m₁ * m₂) / (m₁ + m₂), where m₁ and m₂ are the masses of the two objects. It's used when analyzing the motion of two objects as if they were a single object with this effective mass.
How does using reduced mass simplify calculations in a two-body system?
Instead of tracking the individual motion of two objects interacting with each other, using the reduced mass allows us to treat the system as a single, equivalent object orbiting a fixed point. This greatly simplifies the mathematics, particularly for systems with central forces like gravity.
Can reduced mass ever be equal to the mass of one of the objects? If so, under what circumstances?
Yes, if one object's mass is significantly larger than the other's, the reduced mass will be approximately equal to the mass of the smaller object. The larger mass is essentially stationary relative to the smaller one.
What are some real-world applications where the concept of reduced mass is essential?
Reduced mass is crucial in analyzing molecular vibrations (like stretching and bending), calculating the energy levels of diatomic molecules, and understanding the orbits of planets around stars. It helps to model complex two-body interactions in many physical systems.
So, there you have it! Hopefully, this clears up any confusion about reduced mass and its applications. It might seem a little abstract at first, but understanding how to calculate and use the concept of reduced mass can really simplify things when you're dealing with systems of two bodies. Now go forth and conquer those physics problems!