Moles and Molar Mass: Step-by-Step Calculations

The fundamental relationship between moles and molar mass is a cornerstone in quantitative chemical analysis, enabling precise conversions between mass and number of particles. Avogadro's number, a universal constant with a value of approximately 6.022 x 10²³, defines the number of entities (atoms, molecules, ions, etc.) in one mole, illustrating the scale at which chemists like Marie Curie operated when measuring and manipulating minuscule amounts of radioactive elements. Stoichiometry, a branch of chemistry, uses these mole relationships to predict the quantitative relationships in chemical reactions, often performed in laboratory settings from academic institutions to industrial research facilities. Balances, like those manufactured by Mettler Toledo, are critical instruments for accurately measuring the mass required for molar mass calculations and subsequent mole determinations, impacting the reliability of experimental results.

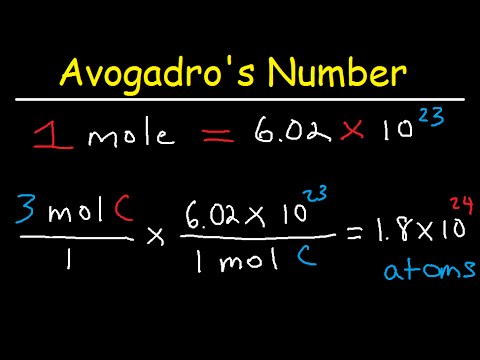
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Avogadro's Number, The Mole, Grams, Atoms, Molar Mass Calculations - Introduction .

The mole (mol) stands as the cornerstone for quantifying matter in chemistry. It is the fundamental unit used to express the amount of a chemical substance. Its existence bridges the vast gap between the infinitesimally small world of atoms and molecules and the tangible, measurable quantities that chemists work with daily in the laboratory. Without the mole concept, quantitative analysis in chemistry would be virtually impossible.

Defining the Mole: The SI Unit for Amount of Substance

The mole is defined as the amount of a substance that contains as many entities (atoms, molecules, ions, electrons, or other specified particles) as there are atoms in exactly 12 grams of carbon-12 (¹²C). This number is known as Avogadro's number, approximately 6.022 x 10²³. The abbreviation for mole is "mol." It's crucial to remember that "mole" refers to a specific number of things, much like "dozen" refers to 12.

The Mole's Significance in Quantitative Chemistry

The mole's true power lies in its ability to connect the microscopic with the macroscopic. Imagine trying to conduct a chemical reaction by counting out individual atoms – an absurd proposition. The mole provides a practical way to relate the number of atoms or molecules to a measurable mass. By knowing the molar mass of a substance (grams per mole), chemists can easily convert between mass and the number of particles, which is essential for stoichiometry, solution preparation, and many other vital calculations. This link is the bedrock of quantitative chemistry.

Consider, for example, synthesizing a compound. A chemist needs to know precisely how much of each reactant to mix to ensure the reaction proceeds efficiently and produces the desired product. Using the mole concept and stoichiometry allows for those precise calculations, ensuring minimal waste and maximum yield.

A Brief History: Avogadro's Contribution

While the mole concept wasn't formally defined until later, its roots lie in the work of Amedeo Avogadro, an Italian scientist whose hypothesis revolutionized our understanding of gases. In 1811, Avogadro proposed that equal volumes of all gases, at the same temperature and pressure, contain the same number of molecules. While Avogadro himself didn't determine the exact number of particles in a given amount of gas, his hypothesis laid the groundwork for understanding the relationship between volume, number of particles, and ultimately, the concept of the mole as we know it today. His contribution was monumental. The constant that bears his name is essential to modern chemistry.

Having established the mole as the fundamental counting unit in chemistry, it's time to introduce a crucial concept that links the number of moles to a tangible property: mass. This bridge is built by the molar mass, a critical tool for any chemist.

Defining Molar Mass: Connecting Mass and Moles

The molar mass is defined as the mass of one mole of a substance. It is typically expressed in grams per mole (g/mol). Understanding molar mass is essential for converting between the mass of a substance and the number of moles it contains, and vice-versa.

This conversion capability is the cornerstone of quantitative chemistry, enabling precise calculations for reactions and experiments.

Molar Mass vs. Atomic Mass vs. Molecular Weight

It's important to distinguish between molar mass, atomic mass, and molecular weight, as these terms are closely related but not identical.

Atomic Mass

Atomic mass refers to the mass of a single atom of an element, typically expressed in atomic mass units (amu). The atomic mass is essentially the weighted average of the masses of all the naturally occurring isotopes of that element.

This value can be found directly on the periodic table.

Molecular Weight (or Formula Weight)

Molecular weight (or formula weight) refers to the sum of the atomic masses of all the atoms in a molecule or formula unit. Like atomic mass, it is expressed in amu.

For example, the molecular weight of water (H₂O) is approximately 18.01 amu (2 x atomic mass of H + atomic mass of O).

The Key Relationship

The molar mass, atomic mass, and molecular weight are intimately connected. The numerical value of the molar mass (in g/mol) is equal to the numerical value of the atomic mass (in amu) or molecular weight (in amu).

However, it is the units that distinguish them.

For instance, the atomic mass of carbon is approximately 12.01 amu, while the molar mass of carbon is approximately 12.01 g/mol. This relationship provides a direct bridge between the microscopic (amu) and the macroscopic (grams) scales.

Using the Periodic Table to Determine Atomic Masses

The periodic table is your most essential tool for determining atomic masses and, consequently, molar masses. Each element on the periodic table is typically displayed with its atomic number and atomic mass.

The atomic mass is the decimal number shown below the element symbol.

For example, the atomic mass of sodium (Na) is approximately 22.99 amu. Therefore, the molar mass of sodium is approximately 22.99 g/mol.

When calculating the molar mass of a compound, you simply add the atomic masses of each element in the compound, multiplied by their respective subscripts in the chemical formula.

This simple, yet powerful application of the periodic table is fundamental to performing accurate mole calculations.

Having mastered the art of linking mass to moles via molar mass, we now turn our attention to connecting moles to the number of individual particles present. This is where Avogadro's Number enters the stage, enabling us to count the otherwise invisible.

Avogadro's Number: Counting the Invisible

While the mole provides a convenient unit for weighing out substances, understanding chemical reactions often requires knowing the number of individual atoms, molecules, or ions involved. This is where Avogadro's Number becomes indispensable.

Avogadro's number is the bridge from the macroscopic world of grams and moles to the microscopic world of individual atoms and molecules.

Defining Avogadro's Number (N_A)

Avogadro's number (N_A) is defined as the number of entities (atoms, molecules, ions, etc.) in one mole of a substance. Its value is approximately 6.022 x 10²³.

Think of it like this: just as a "dozen" always means 12, a "mole" always means 6.022 x 10²³ entities.

This immense number reflects the incredibly small size of individual atoms and molecules.

The Significance of Avogadro's Number in Conversions

Avogadro's number is more than just a definition; it's a powerful conversion factor. It allows us to convert between the number of moles of a substance and the number of individual particles it contains.

The relationship is simple:

Number of particles = Number of moles x Avogadro's Number

Or, conversely:

Number of moles = Number of particles / Avogadro's Number

Examples of Mole Conversions Using Avogadro's Number

Let's illustrate with examples:

Example 1: How many atoms are there in 0.5 moles of iron (Fe)?

Solution: Number of Fe atoms = 0.5 moles x (6.022 x 10²³ atoms/mole) = 3.011 x 10²³ atoms.

Example 2: How many moles are present in 1.204 x 10²⁴ molecules of water (H₂O)?

Solution: Number of moles of H₂O = (1.204 x 10²⁴ molecules) / (6.022 x 10²³ molecules/mole) = 2.0 moles.

These simple calculations highlight the utility of Avogadro's number in bridging the gap between the mole concept and the number of individual particles. By employing this conversion factor, chemists can precisely quantify the composition of matter at the atomic level.

Mastery of this skill is vital for success in quantitative chemistry.

Calculating Molar Mass: A Step-by-Step Guide

Having bridged the gap between moles and individual particles, our attention now shifts to the practical application of calculating molar mass. Accurate calculations of molar mass are essential for quantitative analysis and a firm grasp on chemical calculations.

This section offers a comprehensive, step-by-step guide on how to derive molar mass from chemical formulas, equipping you with the necessary skills for tackling chemical calculations with confidence.

Understanding Chemical Formulas: A Prerequisite

Before diving into the calculations, it's essential to have a firm understanding of chemical formulas.

A chemical formula represents the types and numbers of atoms present in a molecule or compound.

Subscripts indicate the number of atoms of each element in the compound.

For instance, H₂O indicates that a water molecule contains two hydrogen atoms and one oxygen atom.

Understanding these formulas is the cornerstone for calculating molar mass accurately.

Step-by-Step Instructions for Calculating Molar Mass

Calculating molar mass involves a straightforward process:

1. Identify the Chemical Formula: Determine the correct chemical formula for the compound.
2. Find Atomic Masses: Obtain the atomic mass of each element in the compound from the periodic table. These values are typically found below the element symbol.
3. Multiply Atomic Masses by Subscripts: Multiply the atomic mass of each element by its subscript in the chemical formula. If no subscript is present, it is assumed to be 1.
4. Sum the Results: Add up the results from step 3 for all the elements in the compound. The total is the molar mass of the compound in grams per mole (g/mol).

Examples of Molar Mass Calculations

Let's illustrate the process with some common compounds:

Water (H₂O)

• Atomic mass of Hydrogen (H): 1.008 g/mol
• Atomic mass of Oxygen (O): 16.00 g/mol

Molar mass of H₂O = (2 x 1.008 g/mol) + (1 x 16.00 g/mol) = 18.016 g/mol

Sodium Chloride (NaCl)

• Atomic mass of Sodium (Na): 22.99 g/mol
• Atomic mass of Chlorine (Cl): 35.45 g/mol

Molar mass of NaCl = (1 x 22.99 g/mol) + (1 x 35.45 g/mol) = 58.44 g/mol

Glucose (C₆H₁₂O₆)

• Atomic mass of Carbon (C): 12.01 g/mol
• Atomic mass of Hydrogen (H): 1.008 g/mol
• Atomic mass of Oxygen (O): 16.00 g/mol

Molar mass of C₆H₁₂O₆ = (6 x 12.01 g/mol) + (12 x 1.008 g/mol) + (6 x 16.00 g/mol) = 180.156 g/mol

Ethanol (C₂H₅OH)

• Atomic mass of Carbon (C): 12.01 g/mol
• Atomic mass of Hydrogen (H): 1.008 g/mol
• Atomic mass of Oxygen (O): 16.00 g/mol

Molar mass of C₂H₅OH = (2 x 12.01 g/mol) + (6 x 1.008 g/mol) + (1 x 16.00 g/mol) = 46.068 g/mol

Ammonia (NH₃)

• Atomic mass of Nitrogen (N): 14.01 g/mol
• Atomic mass of Hydrogen (H): 1.008 g/mol

Molar mass of NH₃ = (1 x 14.01 g/mol) + (3 x 1.008 g/mol) = 17.034 g/mol

Special Cases: Calculating Molar Mass of Hydrates

Hydrates are compounds that have a specific number of water molecules associated with each formula unit.

For example, Copper(II) sulfate pentahydrate (CuSO₄•5H₂O) has five water molecules for every one CuSO₄ unit.

To calculate the molar mass of a hydrate, you must include the mass of the water molecules.

Molar mass of CuSO₄•5H₂O = Molar mass of CuSO₄ + (5 x Molar mass of H₂O)

Molar mass of CuSO₄ = 63.55 + 32.07 + (4 x 16.00) = 159.62 g/mol

Molar mass of 5H₂O = 5 x 18.016 g/mol = 90.08 g/mol

Molar mass of CuSO₄•5H₂O = 159.62 g/mol + 90.08 g/mol = 249.70 g/mol

By meticulously following these steps and understanding the nuances of chemical formulas, including those of hydrates, you can confidently calculate the molar mass of a wide range of compounds.

This skill is foundational for more advanced stoichiometric calculations and understanding chemical reactions at a quantitative level.

Mastering Mole Conversions: From Mass to Moles and Back Again

With a firm grasp on molar mass, we can now tackle the critical skill of mole conversions. These conversions allow us to move seamlessly between the macroscopic world of measurable mass and the microscopic world of atoms and molecules.

This section will equip you with the tools and understanding necessary to perform these essential calculations.

Converting Between Mass and Moles Using Molar Mass

The molar mass serves as the bridge between mass and moles. It provides the conversion factor needed to translate grams into moles and vice versa.

Recall that molar mass is expressed in grams per mole (g/mol). This unit inherently suggests the conversion process.

Mass to Moles Conversion

To convert from mass (in grams) to moles, you'll use the following formula:

Moles = Mass (g) / Molar Mass (g/mol)

This equation indicates that you divide the given mass by the molar mass of the substance to find the corresponding number of moles.

For example, let's convert 50.0 grams of water (H₂O) to moles. We know that the molar mass of water is approximately 18.016 g/mol.

Moles of H₂O = 50.0 g / 18.016 g/mol = 2.775 mol

Moles to Mass Conversion

Conversely, to convert from moles to mass, you'll use this formula:

Mass (g) = Moles x Molar Mass (g/mol)

Here, you multiply the number of moles by the molar mass to find the corresponding mass in grams.

For example, let's convert 3.00 moles of sodium chloride (NaCl) to grams. The molar mass of NaCl is approximately 58.44 g/mol.

Mass of NaCl = 3.00 mol x 58.44 g/mol = 175.32 g

Converting Between Moles and Number of Particles Using Avogadro's Number

Avogadro's number (6.022 x 10²³) provides the link between the number of moles and the number of individual particles (atoms, molecules, ions, etc.).

It tells us how many particles are present in one mole of any substance.

Moles to Particles Conversion

To convert from moles to the number of particles, use the following formula:

Number of Particles = Moles x Avogadro's Number

Multiply the number of moles by Avogadro's number to find the total number of particles.

For example, let's calculate the number of molecules in 0.50 moles of carbon dioxide (CO₂).

Number of CO₂ molecules = 0.50 mol x 6.022 x 10²³ molecules/mol = 3.011 x 10²³ molecules

Particles to Moles Conversion

To convert from the number of particles to moles, use this formula:

Moles = Number of Particles / Avogadro's Number

Divide the number of particles by Avogadro's number to find the corresponding number of moles.

For example, let's calculate the number of moles in 1.204 x 10²⁴ atoms of iron (Fe).

Moles of Fe = 1.204 x 10²⁴ atoms / 6.022 x 10²³ atoms/mol = 2.00 mol

Multi-Step Conversions: Combining Mass-to-Mole and Mole-to-Particle Conversions

Often, you'll need to perform conversions that involve both mass-to-mole and mole-to-particle steps.

These multi-step conversions require careful planning and execution, but they are essential for solving complex chemical problems.

The key is to use molar mass to get to moles, and then Avogadro's number to convert to the number of particles (or vice versa).

For example, let's determine the number of hydrogen atoms in 10.0 grams of water (H₂O). This requires a two-step process:

1. Convert mass of H₂O to moles of H₂O:

   Moles of H₂O = 10.0 g / 18.016 g/mol = 0.555 mol

2. Convert moles of H₂O to number of H atoms:

   Since each water molecule has 2 hydrogen atoms, we multiply the number of moles of water by 2 and then by Avogadro's number.

   Number of H atoms = 0.555 mol H₂O x 2 mol H/mol H₂O x 6.022 x 10²³ H atoms/mol H = 6.68 x 10²³ H atoms

By mastering these individual conversions and combining them strategically, you can confidently navigate a wide range of stoichiometric problems and gain a deeper understanding of the quantitative relationships in chemistry.

Applications of the Mole Concept: Where Moles Matter

The mole concept isn't just a theoretical construct; it's the workhorse behind countless calculations and analyses in chemistry. Its true power lies in its practical applications, providing a quantitative framework for understanding chemical reactions and compositions. This section delves into some of the most significant areas where the mole concept plays a crucial role.

Stoichiometry: The Language of Chemical Reactions

Stoichiometry is the branch of chemistry that deals with the quantitative relationships between reactants and products in chemical reactions. It allows us to predict the amounts of reactants needed and products formed in a chemical reaction, all thanks to the mole.

Mole Ratios and Balanced Chemical Equations

At the heart of stoichiometry lies the balanced chemical equation. This equation provides the mole ratios between all substances involved in the reaction. These ratios serve as conversion factors, allowing us to calculate the amount of one substance required to react with or produce a specific amount of another.

For example, consider the balanced equation for the synthesis of ammonia:

N₂(g) + 3H₂(g) → 2NH₃(g)

This equation tells us that one mole of nitrogen gas reacts with three moles of hydrogen gas to produce two moles of ammonia gas. The coefficients in front of each chemical formula represent the mole ratios.

Identifying the Limiting Reactant

In most chemical reactions, reactants are not present in exact stoichiometric ratios. This means that one reactant will be completely consumed before the others. This reactant is known as the limiting reactant because it limits the amount of product that can be formed.

To identify the limiting reactant, you must first calculate the number of moles of each reactant present. Then, use the stoichiometric ratios to determine which reactant would produce the least amount of product. This reactant is the limiting reactant.

The other reactants are considered to be in excess, as some of them will be left over after the reaction is complete.

Yield: Theoretical, Actual, and Percent

Theoretical yield is the maximum amount of product that can be formed from a given amount of limiting reactant, assuming perfect reaction conditions. However, in reality, the amount of product obtained, known as the actual yield, is often less than the theoretical yield. This is due to factors such as incomplete reactions, side reactions, and loss of product during purification.

The percent yield is a measure of the efficiency of a chemical reaction and is calculated as follows:

Percent Yield = (Actual Yield / Theoretical Yield) x 100%

A higher percent yield indicates a more efficient reaction.

Percent Composition: Unveiling the Elemental Makeup

Percent composition tells us the percentage by mass of each element in a compound. It is a practical application of the mole concept and molar mass.

To calculate the percent composition of an element in a compound, you divide the total mass of that element in one mole of the compound by the molar mass of the compound and multiply by 100%:

Percent Composition = (Mass of Element in 1 mole of Compound / Molar Mass of Compound) x 100%

For example, consider water (H₂O). The molar mass of water is approximately 18.016 g/mol. The mass of hydrogen in one mole of water is approximately 2.016 g (2 x 1.008 g/mol), and the mass of oxygen is approximately 16.00 g/mol.

Therefore, the percent composition of hydrogen in water is (2.016 g / 18.016 g) x 100% = 11.19%, and the percent composition of oxygen is (16.00 g / 18.016 g) x 100% = 88.79%.

Empirical Formula Determination: Finding the Simplest Ratio

The empirical formula represents the simplest whole-number ratio of atoms in a compound. Determining the empirical formula from experimental data is another important application of the mole concept.

The process typically involves converting mass percentages (obtained from elemental analysis) to moles, then dividing each mole value by the smallest mole value to obtain a simple mole ratio. If the resulting ratios are not whole numbers, they are multiplied by a common factor to obtain whole numbers. These whole numbers become the subscripts in the empirical formula.

For instance, suppose a compound is found to contain 40.0% carbon, 6.7% hydrogen, and 53.3% oxygen by mass. Converting these percentages to moles (assuming 100g of the compound), we divide by the respective atomic masses (C: 12.01 g/mol, H: 1.008 g/mol, O: 16.00 g/mol). We get roughly 3.33 moles of C, 6.64 moles of H, and 3.33 moles of O. Dividing by the smallest (3.33), we obtain a ratio of 1:2:1, leading to the empirical formula CH₂O.

Solutions and Molarity: Quantifying Concentration

In chemistry, solutions are ubiquitous. Molarity (M) is a common way to express the concentration of a solution, defined as the number of moles of solute per liter of solution:

Molarity (M) = Moles of Solute / Liters of Solution

The mole concept is essential for preparing solutions of specific concentrations and for performing calculations involving solution stoichiometry. For instance, if you need to prepare 500 mL of a 0.1 M solution of NaCl, you would first calculate the number of moles of NaCl required (0.1 mol/L x 0.5 L = 0.05 mol). Then, you would weigh out the corresponding mass of NaCl (0.05 mol x 58.44 g/mol = 2.922 g) and dissolve it in enough water to make a total volume of 500 mL.

These applications highlight the pervasive role of the mole concept in quantitative chemical analysis. By mastering these principles, you unlock the ability to make meaningful predictions and calculations about the behavior of matter in chemical systems.

Experimental Determination of Molar Mass: Finding Molar Mass in the Lab

While molar mass can be readily calculated from a compound's chemical formula and the periodic table, experimental determination provides a crucial link between theoretical calculations and real-world substances. Several laboratory techniques allow us to determine the molar mass of an unknown compound, each relying on different physical principles. These methods are particularly important when dealing with newly synthesized compounds or substances with unknown or uncertain composition.

The Gas Density Method: Leveraging the Ideal Gas Law

The gas density method relies on the relationship between the density of a gas, its pressure, temperature, and molar mass, as described by the Ideal Gas Law. This method is applicable to volatile substances that can be readily converted into a gaseous state without decomposition.

Experimental Setup and Procedure

The experimental setup typically involves a known volume of gas at a measured temperature and pressure. The mass of the gas is also carefully determined. By precisely controlling and measuring these variables, we can use the Ideal Gas Law to calculate the gas's molar mass.

Calculation Using the Ideal Gas Law

The Ideal Gas Law is expressed as:

PV = nRT

Where:

• P = Pressure
• V = Volume
• n = Number of moles
• R = Ideal gas constant (0.0821 L atm / (mol K))
• T = Temperature (in Kelvin)

Since n = mass / molar mass (m/M), we can rearrange the Ideal Gas Law to solve for molar mass (M):

M = (mRT) / PV

By plugging in the experimentally determined values for mass (m), pressure (P), volume (V), and temperature (T), we can calculate the molar mass (M) of the gas.

Limitations of the Gas Density Method

It's important to note that the Ideal Gas Law is an approximation that works best at low pressures and high temperatures. Deviations from ideal behavior can lead to inaccuracies in the determined molar mass. This method is also unsuitable for substances that decompose or react at the temperatures required for vaporization.

Colligative Properties: Exploiting Solution Behavior

Colligative properties are properties of solutions that depend on the concentration of solute particles, rather than the nature of the solute itself. Several colligative properties, such as freezing point depression and boiling point elevation, can be used to determine the molar mass of a solute.

Freezing Point Depression

The freezing point of a solution is lower than that of the pure solvent. The extent of this depression is proportional to the molality of the solute (moles of solute per kilogram of solvent).

ΔTf = Kf

**m

Where:

• ΔTf = Freezing point depression
• Kf = Cryoscopic constant (freezing point depression constant) of the solvent
• m = Molality of the solution

By measuring the freezing point depression and knowing the Kf value for the solvent, the molality of the solution can be calculated. From the molality and the mass of the solute and solvent, the molar mass of the solute can be determined.

Boiling Point Elevation

Similarly, the**boiling point

**of a solution is higher than that of the pure solvent. The extent of this elevation is also proportional to the molality of the solute.

ΔTb = Kb** m

Where:

• ΔTb = Boiling point elevation
• Kb = Ebullioscopic constant (boiling point elevation constant) of the solvent
• m = Molality of the solution

Analogous to freezing point depression, measuring the boiling point elevation and knowing the Kb value allows for the calculation of molality and, subsequently, the molar mass of the solute.

Experimental Considerations for Colligative Properties

Accurate temperature measurements are crucial for both freezing point depression and boiling point elevation methods. The solute must be non-volatile in the boiling point elevation method. Furthermore, the solution should be dilute to ensure that the colligative properties behave ideally. Solute association or dissociation in the solvent can also complicate the analysis.

Choosing the Right Method

The choice of method for experimental molar mass determination depends on the properties of the substance being studied. The gas density method is suitable for volatile substances, while colligative property methods are applicable to solutes dissolved in a solvent. Understanding the principles and limitations of each technique is essential for obtaining accurate and reliable results.

Tools and Resources for Mole Calculations: Your Chemistry Toolkit

Successfully navigating the world of mole calculations requires more than just understanding the concepts. Having the right tools and resources readily available can significantly improve accuracy and efficiency. This section highlights essential aids for mastering mole calculations, ranging from calculators to textbooks and online tutorials.

The Indispensable Scientific Calculator

A scientific calculator is an absolute necessity for any chemistry student or professional. Look for a calculator with the following features:

• Exponential notation: Essential for handling Avogadro's number and very small or large quantities.
• Logarithmic functions: Useful for pH calculations and other advanced chemistry topics.
• Memory functions: Allow you to store intermediate results for complex calculations.
• Trigonometric functions: Though less directly related to mole calculations, they are important for general chemistry problem-solving.

While advanced graphing calculators are useful, a solid scientific calculator is sufficient for most mole-related calculations. Models from Texas Instruments (TI-30XS MultiView) and Casio (fx-991 series) are known for their reliability and features.

Online Molar Mass Calculators: Instant Solutions at Your Fingertips

Several excellent online molar mass calculators can save time and reduce errors. These tools automatically calculate the molar mass of a compound when you input its chemical formula.

• WebQC's Molar Mass Calculator: A clean, user-friendly interface.
• Sigma-Aldrich's Molar Mass Calculator: A reliable resource from a trusted chemical supplier.
• CalculatorSoup's Molar Mass Calculator: Offers additional features like percent composition calculations.

When using online calculators, be sure to double-check the chemical formula you enter to avoid errors. While these calculators are convenient, it's crucial to understand the underlying principles of molar mass calculation rather than relying solely on them.

Chemistry Textbooks: A Foundation of Knowledge

A well-written chemistry textbook provides a comprehensive understanding of the mole concept and its applications. Here are some recommended textbooks:

• Chemistry: The Central Science by Brown, LeMay, Bursten, Murphy, and Woodward: A classic and widely used textbook covering all essential chemistry topics.
• General Chemistry by Petrucci, Herring, Madura, and Bissonnette: Known for its clear explanations and detailed examples.
• Chemistry by Zumdahl and Zumdahl: A popular choice for its problem-solving approach and engaging writing style.

Choose a textbook that aligns with your learning style and the level of your chemistry course. Use it as a primary reference for understanding concepts and practicing problems.

Online Chemistry Tutorials: Learning at Your Own Pace

Online chemistry tutorials offer an accessible and flexible way to learn and review the mole concept. These resources often include video lectures, interactive exercises, and practice quizzes.

• Khan Academy Chemistry: Offers comprehensive chemistry content, including videos, articles, and practice exercises, covering the mole concept and related topics.
• Chem LibreTexts: A collaborative project providing open-access chemistry textbooks and learning materials.
• MIT OpenCourseWare: Offers lecture notes and problem sets from MIT's chemistry courses.
• Crash Course Chemistry: Fast-paced and engaging videos covering various chemistry topics, including moles.

Use these online resources to supplement your textbook and classroom learning. They can be particularly helpful for visualizing concepts and working through practice problems.

Common Mistakes and How to Avoid Them: Troubleshooting Mole Calculations

Mastering mole calculations is a fundamental skill in chemistry, but even seasoned students can fall prey to common errors. Recognizing these pitfalls and understanding how to avoid them is crucial for achieving accuracy and building confidence. This section will dissect common mistakes related to chemical formulas, atomic masses, balanced equations, and unit handling, providing practical strategies for error prevention.

Misinterpreting Chemical Formulas: A Recipe for Disaster

The chemical formula serves as the blueprint for a compound, and misreading it is a frequent source of error. This can manifest in several ways.

One common mistake is confusing subscripts, which indicate the number of atoms of each element in a molecule. For instance, H₂O is not the same as HO₂—the former is water, while the latter is a completely different (and unstable) molecule.

Another pitfall involves correctly interpreting parentheses in formulas like Mg(OH)₂. The subscript outside the parentheses applies to all elements within, meaning there are two oxygen atoms and two hydrogen atoms.

Finally, students sometimes struggle with hydrates, such as CuSO₄·5H₂O. The "·5H₂O" indicates that for every one unit of copper(II) sulfate, there are five water molecules associated with it. When calculating molar mass, include the mass of all five water molecules.

Avoiding Formula Errors

To avoid these errors, take the time to carefully examine each chemical formula. Double-check subscripts and ensure that parentheses are correctly interpreted. When dealing with hydrates, remember to include the water molecules in your calculations.

The Perils of Incorrect Atomic Masses

Molar mass calculations rely on accurate atomic masses, typically obtained from the periodic table. Using outdated or rounded-off values can introduce significant errors, particularly in complex calculations.

Students should use the most precise atomic masses available, often found on detailed periodic tables or online databases like the NIST Atomic Weights and Isotopic Compositions Database. Using at least four significant figures is generally recommended for accurate results.

Precision is Key

Always use a reliable and up-to-date periodic table. Avoid rounding atomic masses prematurely, as this can compound errors in subsequent calculations. Use the full precision offered by your calculator.

The Importance of Balanced Chemical Equations

Stoichiometry, which relies on mole ratios, is entirely dependent on balanced chemical equations. Forgetting to balance an equation or doing so incorrectly will lead to incorrect mole ratios and, consequently, inaccurate results.

The coefficients in a balanced equation represent the relative number of moles of each reactant and product involved in the reaction. An unbalanced equation does not accurately reflect the stoichiometry of the reaction.

Balancing Act: Tips for Success

Before performing any stoichiometric calculations, always double-check that your chemical equation is balanced. A systematic approach, such as using the "balancing by inspection" method or the algebraic method, can help avoid errors.

For complex reactions, consider using online equation balancers to verify your work, but always understand the underlying principles.

Units: The Silent Saboteurs of Calculations

One of the most pervasive errors in mole calculations is neglecting or mismanaging units. Failing to include units or using the wrong units can lead to answers that are off by orders of magnitude.

Remember that molar mass is expressed in grams per mole (g/mol), and volume is often measured in liters (L) or milliliters (mL). It's crucial to ensure that all quantities are expressed in compatible units before performing calculations.

Unit Conversion and Dimensional Analysis

Always include units in every step of your calculation. Use dimensional analysis (also known as the factor-label method) to track units and ensure that they cancel correctly. This technique involves multiplying by conversion factors to change from one unit to another.

For example, to convert grams to moles, multiply by the reciprocal of the molar mass (mol/g). If the units don't cancel out to give you the desired unit, you've likely made an error.

By recognizing these common pitfalls and adopting meticulous habits, students can significantly improve their accuracy and confidence in tackling mole calculations. Careful attention to detail and a strong understanding of fundamental concepts are the keys to success.

Video: Moles and Molar Mass: Step-by-Step Calculations

Play Video

So, there you have it! Calculating with moles and molar mass might seem tricky at first, but with a little practice, you'll be converting grams to moles (and back again!) like a pro. Now go forth and conquer those chemistry calculations!