Discounting Factor Calculator .biz: Smart Guide

Discounting Factor Calculator .biz emerges as an essential tool in financial analysis, particularly for entities navigating complex investment decisions. The Time Value of Money, a fundamental concept in finance, dictates that a sum of money is worth more now than the same sum will be at a future date due to its earnings potential in the interim. Bloomberg terminals, widely used by financial professionals, often incorporate discounting factor calculations to evaluate investment opportunities. For instance, a corporation might use a discounting factor calculator .biz to determine the present value of future cash flows from a potential project, ensuring optimal capital allocation. The expertise of a Chartered Financial Analyst (CFA) often involves utilizing this tool to advise clients on making informed investment decisions.

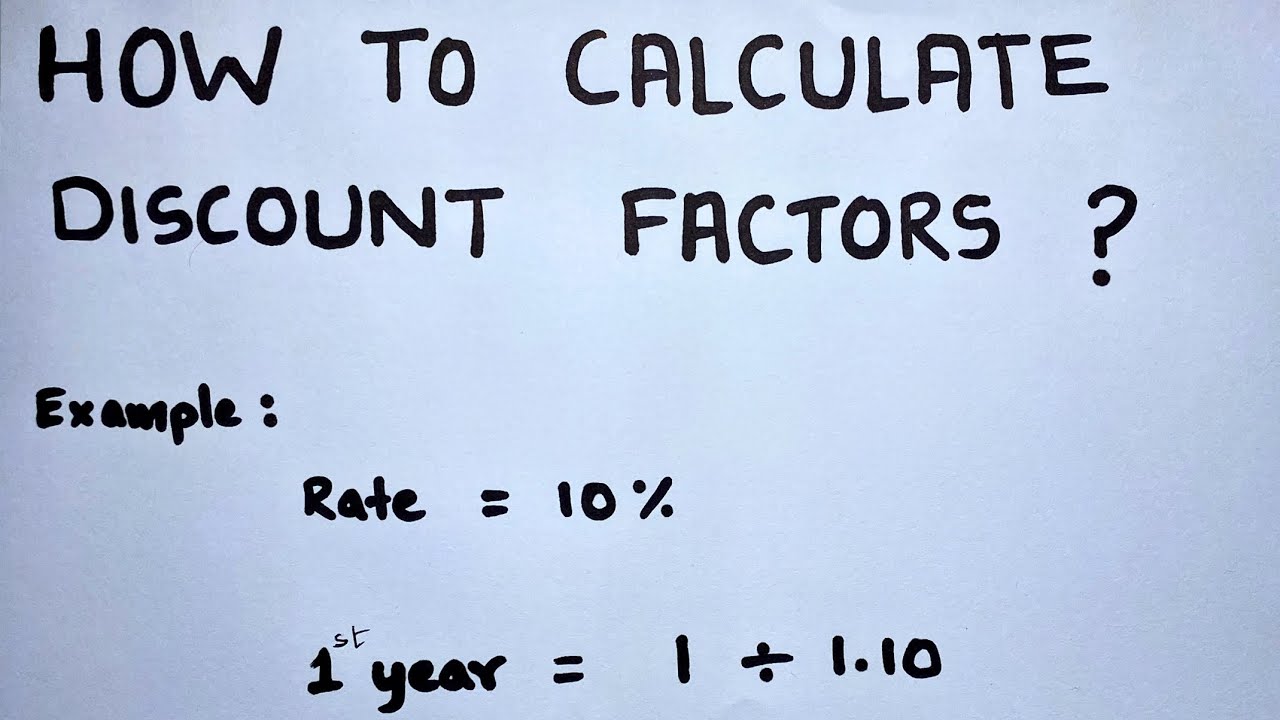
Image taken from the YouTube channel Saheb Academy , from the video titled How to Calculate Discount Factors? (Normal and Scientific) .

At the heart of sound financial decision-making lies the principle of discounting, a powerful technique that translates future monetary values into their present-day equivalents. It's a cornerstone of financial analysis, enabling us to compare and evaluate opportunities across different time horizons. Discounting provides a framework for understanding the true cost and benefit of choices involving future cash flows.

The Essence of Discounting

In its simplest form, discounting is the process of determining the present value of a future sum of money. It acknowledges that a dollar received today is intrinsically more valuable than a dollar received in the future. This seemingly simple concept has profound implications for investment decisions, project evaluation, and long-term financial planning.

Time Value of Money: The Foundation

The rationale behind discounting rests on the fundamental concept of the Time Value of Money (TVM). TVM posits that money available today possesses greater worth due to its potential earning capacity. This earning capacity stems from the opportunity to invest the money and generate returns over time.

Therefore, receiving money today allows you to begin accumulating interest or profits immediately. Waiting to receive that same amount means foregoing those potential earnings, diminishing its real value. The longer you wait, the less valuable that future sum becomes in today's terms.

Inflation erodes purchasing power over time. This is another key reason why today's money is more valuable than tomorrow's.

Discounting: A Critical Tool in Financial Decision-Making

Discounting plays a pivotal role in a wide range of financial decisions. Its applications include:

• Investment Appraisal: Discounting allows investors to assess the profitability and feasibility of potential investments. By comparing the present value of expected future cash flows to the initial investment cost, investors can make informed choices about where to allocate capital.

• Capital Budgeting: Companies use discounting to evaluate and select the most profitable projects. By comparing the present values of different investment opportunities, companies can prioritize projects that maximize shareholder wealth.

• Retirement Planning: Individuals use discounting to determine the present value of future retirement income streams. This helps them plan for their financial needs during retirement and determine how much they need to save today to achieve their retirement goals.

By understanding and applying the principles of discounting, individuals and organizations can make more informed and effective financial decisions, optimizing resource allocation and maximizing long-term value.

Decoding the Discounting Toolkit: Key Concepts Explained

At the heart of sound financial decision-making lies the principle of discounting, a powerful technique that translates future monetary values into their present-day equivalents. It's a cornerstone of financial analysis, enabling us to compare and evaluate opportunities across different time horizons. Discounting provides a framework for understanding the time value of money, acknowledging that a dollar today is worth more than a dollar tomorrow. This section unpacks the core concepts that form the foundation of discounting, providing you with the knowledge to effectively wield this financial tool.

Understanding the Discount Rate

The discount rate is arguably the most critical component of the discounting process. It's the rate used to convert future cash flows into their present value, effectively reflecting the opportunity cost of capital and the inherent risk associated with receiving those future cash flows.

Components of the Discount Rate

The discount rate isn't simply a number pulled out of thin air. It's typically comprised of two key elements:

• Risk-Free Rate: This is the theoretical rate of return of an investment with zero risk. In practice, it's often represented by the yield on a government bond, such as a U.S. Treasury bond, as these are considered virtually default-free.

• Risk Premium: This component compensates investors for the uncertainty and potential risks associated with the specific cash flows being discounted. The higher the perceived risk, the higher the risk premium demanded by investors. This premium could account for factors like market volatility, company-specific risks, or project uncertainties.

The formula for calculating the discount rate can be represented as:

Discount Rate = Risk-Free Rate + Risk Premium

The Impact of the Discount Rate on Present Value

A crucial relationship to understand is the inverse correlation between the discount rate and the calculated present value. Simply put, a higher discount rate will result in a lower present value, and vice-versa.

This occurs because a higher discount rate reflects a greater degree of risk or a higher opportunity cost. Investors demand a lower price (present value) for future cash flows when they perceive a higher level of risk.

Delving into Present Value (PV)

Present Value (PV) represents the current worth of a future sum of money or a stream of cash flows, given a specified rate of return (the discount rate). It essentially answers the question: "What is this future amount worth to me today?".

The significance of present value lies in its ability to provide a common basis for comparing investment opportunities or evaluating financial obligations. It allows you to make informed decisions by bringing all future values back to a single point in time: the present.

The fundamental formula for calculating present value is:

PV = FV / (1 + r)^n

Where:

• PV = Present Value
• FV = Future Value
• r = Discount Rate
• n = Number of Periods

Exploring Future Value (FV)

Future Value (FV), conversely, represents the value of an asset or investment at a specified date in the future, assuming a certain rate of growth or return.

Understanding the relationship between present value, future value, and the discount rate is crucial. They are intrinsically linked, with the discount rate serving as the bridge between the present and the future. Compounding is the process of calculating future value, while discounting is its inverse.

The formula for calculating future value is:

FV = PV * (1 + r)^n

Where:

• FV = Future Value
• PV = Present Value
• r = Interest Rate
• n = Number of Periods

Annuities: A Stream of Payments

An annuity is defined as a series of equal payments or receipts made at regular intervals over a specified period. Common examples include monthly mortgage payments, annual insurance payouts, or quarterly dividend payments.

Ordinary Annuity vs. Annuity Due

It's important to differentiate between two types of annuities:

• Ordinary Annuity: Payments are made at the end of each period. This is the most common type of annuity.

• Annuity Due: Payments are made at the beginning of each period.

Calculating Present and Future Value of Annuities

The formulas for calculating the present value and future value of annuities differ slightly depending on whether it's an ordinary annuity or an annuity due. These formulas can be found in most finance textbooks or online financial calculators.

Perpetuities: Payments that Last Forever

A perpetuity is a special case of an annuity. It represents a stream of payments that continues indefinitely (i.e., forever). While a true perpetuity is rare in practice, it's a useful concept for valuing assets that are expected to generate a steady stream of income for the foreseeable future.

The formula for calculating the present value of a perpetuity is:

PV = Payment / r

Where:

• PV = Present Value
• Payment = The constant payment received each period
• r = Discount Rate

Net Present Value (NPV): The Ultimate Investment Yardstick

Net Present Value (NPV) is a powerful metric used to assess the profitability of an investment or project. It represents the difference between the present value of cash inflows and the present value of cash outflows over a period of time.

NPV plays a crucial role in investment appraisal and project selection because it provides a clear and unambiguous decision-making criterion. A positive NPV indicates that the investment is expected to generate more value than its cost, while a negative NPV suggests the opposite.

The NPV Decision Rule

The decision rule for NPV is straightforward:

• Accept: If NPV > 0 (indicates a profitable investment)
• Reject: If NPV < 0 (indicates a potential loss)

An NPV of zero suggests that the investment is expected to break even, neither creating nor destroying value.

Practical Discounting Tools: Mastering the Calculators

Having grasped the underlying concepts of discounting, let's now turn our attention to the practical tools that simplify the calculations involved. These calculators, both specialized and general, empower you to quickly and accurately determine present and future values, enabling more informed financial decisions.

Single Cash Flow Discounting Calculator

This tool is the workhorse for determining the present value of a single lump sum payment to be received in the future. It addresses questions like: "What is that $1,000 bonus I'll get in three years really worth today?"

Functionality: The calculator uses the core present value formula: PV = FV / (1 + r)^n, where FV is the future value, r is the discount rate, and n is the number of periods.

Example: Suppose you are promised $1,000 in 5 years, and your discount rate is 5%. Inputting these values yields a present value of approximately $783.53. This means that receiving $1,000 five years from now is equivalent to receiving $783.53 today, given your required rate of return.

Annuity Discounting Calculator

Annuities, representing a series of equal payments over time, require a slightly more complex calculation. This calculator handles both ordinary annuities (payments at the end of each period) and annuities due (payments at the beginning).

Functionality: It uses specialized formulas to calculate the present value (PV) or future value (FV) of an annuity, considering the payment amount, interest rate, and number of periods.

Example: Imagine you are considering an investment that pays $500 per year for 10 years, with a discount rate of 7%. An ordinary annuity calculation reveals a present value of approximately $3,511.77. An annuity due calculation, where payments are received at the beginning of each period, results in a slightly higher present value of around $3,757.60, reflecting the earlier receipt of cash flows.

This highlights the importance of correctly identifying the annuity type (ordinary or due) to ensure accurate valuation.

Perpetuity Discounting Calculator

A perpetuity, a special type of annuity, involves an infinite stream of payments. While seemingly theoretical, perpetuities are useful for valuing assets like preferred stocks or certain types of bonds.

Functionality: The calculator employs the simple formula: PV = Payment / r, where Payment is the constant payment received each period, and r is the discount rate.

Example: If a perpetuity promises to pay $100 per year indefinitely, and your discount rate is 10%, the present value of this perpetuity is $1,000. This means you would be willing to pay $1,000 today for the right to receive $100 every year forever, given your required rate of return.

NPV Calculator

The Net Present Value (NPV) Calculator is critical for evaluating the profitability of investments involving multiple cash inflows and outflows over time. It is especially useful for projects that require an initial investment.

Functionality: The NPV Calculator discounts each individual cash flow back to its present value and then sums them together. It then subtracts the initial investment (usually at time zero). A positive NPV indicates a potentially profitable investment, while a negative NPV suggests the investment might result in a loss.

Example: Consider a project requiring an initial investment of $5,000. It is expected to generate cash flows of $1,500 in year 1, $2,000 in year 2, $2,500 in year 3, and $1,000 in year 4. Assuming a discount rate of 8%, the NPV is calculated as the sum of the present values of all future cashflows, minus the initial investment.

Let's say the calculations determine the total present value of the future cashflows to be $5,300. The NPV would be equal to $5,300 - $5,000 = $300. This indicates the project is expected to generate a profit, in today's dollars, of $300.

Online Calculators (General)

The internet is replete with free online discounting calculators. These offer convenience and accessibility, allowing you to perform calculations on the go.

Availability: Numerous financial websites, academic institutions, and investment firms provide these tools. A simple search for "present value calculator" will yield a plethora of options.

Caution: While convenient, it's essential to verify the accuracy of the results. Different calculators may use slightly different assumptions or rounding methods. Always cross-reference results from multiple sources or with your own manual calculations, especially for complex scenarios.

Reputable sources like Investopedia or corporate finance websites (e.g., those associated with major financial institutions or accounting firms) are generally considered reliable.

Discounting in Action: Real-World Applications

Having equipped ourselves with the conceptual understanding and practical tools of discounting, it's time to explore how these principles translate into tangible benefits across various financial domains. Discounting isn't merely a theoretical exercise; it's a powerful analytical technique that informs critical decisions every day.

Investment Analysis: Gauging Profitability and Feasibility

Discounting lies at the heart of sound investment analysis. By calculating the present value of expected future cash flows and comparing it to the initial investment outlay, we can objectively assess whether a proposed venture is financially viable.

This process reveals whether the anticipated returns are sufficient to justify the risks and opportunity costs associated with the investment.

The Power of Net Present Value (NPV)

The Net Present Value (NPV) metric is paramount in investment decision-making. A positive NPV signifies that the present value of expected cash inflows exceeds the present value of cash outflows, suggesting a potentially profitable investment.

Conversely, a negative NPV indicates that the investment is projected to result in a net loss. Rational investors will generally prioritize projects with the highest positive NPV, as these are expected to generate the greatest returns. However, NPV should not be considered in isolation, and qualitative factors should also be considered.

Capital Budgeting: Maximizing Shareholder Value

Capital budgeting, the process of evaluating and selecting long-term investments, relies heavily on discounting techniques. Companies use discounted cash flow analysis to compare various investment opportunities, striving to allocate capital to projects that will ultimately maximize shareholder wealth.

Discounting enables businesses to objectively rank projects based on their present value, ensuring that resources are directed towards the most promising ventures.

Beyond NPV: The Role of Internal Rate of Return (IRR)

While NPV is a cornerstone of capital budgeting, other discounting-based metrics, such as the Internal Rate of Return (IRR), also play a significant role. IRR represents the discount rate at which the NPV of an investment equals zero.

Projects with an IRR exceeding the company's cost of capital are generally considered acceptable.

However, IRR has limitations (multiple IRRs, scale problems, etc.) and should be used in conjunction with NPV for a comprehensive assessment.

Real Estate Valuation: Assessing Property Worth

Discounting plays a crucial role in real estate valuation, particularly in estimating the fair market value of income-producing properties. The Discounted Cash Flow (DCF) method is a widely used appraisal technique that involves projecting future rental income streams and discounting them back to their present value.

This present value represents the estimated worth of the property, reflecting the anticipated future cash flows it will generate. By discounting expected future rental income, investors can determine a property's current worth, aiding in informed buying or selling decisions.

Retirement Planning: Securing Your Financial Future

Discounting is also invaluable for retirement planning. By projecting future expenses and desired income streams during retirement, individuals can use discounting to determine the present value of these future needs.

This calculation helps to estimate how much they need to save today to ensure a comfortable and financially secure retirement.

Calculating Your Retirement Savings Target

Discounting enables individuals to translate their future retirement goals into a concrete savings target. By considering factors like expected inflation, investment returns, and the desired length of retirement, individuals can calculate the lump sum needed to fund their retirement years.

This present value calculation provides a clear benchmark for tracking progress and making informed savings decisions throughout their working lives.

Expanding the Horizon: Related Financial Domains

Having equipped ourselves with the conceptual understanding and practical tools of discounting, it's time to explore how these principles translate into tangible benefits across various financial domains. Discounting isn't merely a theoretical exercise; it's a powerful analytical technique that informs crucial decisions across a wide spectrum of financial activities. Its influence extends far beyond basic present value calculations, permeating valuation exercises, risk management strategies, and the intricate landscape of financial planning.

Discounting's Pivotal Role in Valuation

At its core, valuation seeks to determine the economic worth of an asset, be it a tangible piece of property, an intangible intellectual property right, or an entire company. Discounting plays a pivotal role in this process, providing the foundational mechanism for translating future expectations into present-day realities. Without discounting, valuation would be relegated to guesswork, lacking the rigorous framework necessary for defensible and reliable assessments.

Essentially, valuation seeks to quantify what a future stream of cash flows, earnings, or other benefits is truly worth today. This quantification relies heavily on the discount rate – the rate used to determine the present value of these future cash flows.

A classic example is the Discounted Cash Flow (DCF) analysis. DCF analysis projects future cash flows and then discounts them back to the present using a discount rate that reflects the riskiness of those cash flows. The sum of these discounted cash flows represents the intrinsic value of the asset or company. The higher the discount rate, the lower the present value, reflecting the principle that riskier investments demand higher returns. Other valuation methods also use discounting, albeit implicitly or indirectly. Understanding discounting principles is, therefore, fundamental to grasping the nuances of valuation.

Discounting and the Art of Risk Management

Risk management is inextricably linked to discounting. Future cash flows are not guaranteed; they are subject to a myriad of uncertainties that can significantly impact their actual value. These uncertainties need to be factored into the discounting process to arrive at a realistic valuation. The discount rate acts as a crucial lever for incorporating risk.

A higher discount rate reflects a greater degree of perceived risk. This increased rate lowers the present value of future cash flows, providing a cushion against potential shortfalls. However, setting the appropriate discount rate is a delicate balancing act. Overly conservative rates can lead to the rejection of potentially profitable investments, while overly optimistic rates can result in disastrous outcomes.

Techniques like sensitivity analysis are invaluable in assessing the impact of different discount rates on investment decisions. By exploring a range of possible discount rates, decision-makers can gain a better understanding of the potential risks and rewards associated with an investment.

Ultimately, effective risk management requires a deep understanding of discounting principles and the ability to incorporate risk assessments into the calculation of present values.

Discounting as a Cornerstone of Financial Planning

Financial planning involves creating a roadmap to achieve long-term financial goals, such as a comfortable retirement, funding a child's education, or accumulating wealth. Discounting plays a cornerstone role in this process by enabling individuals to assess the present value of future needs and resources.

Consider retirement planning, for instance. Individuals need to estimate their future living expenses, account for inflation, and determine how much they need to save today to ensure a financially secure retirement. Discounting allows them to calculate the present value of these future expenses, providing a target savings goal.

Similarly, discounting is essential for evaluating the present value of future income streams, such as pensions or Social Security benefits. By comparing the present value of future resources with the present value of future needs, individuals can identify potential shortfalls and develop strategies to address them.

Effective financial planning relies heavily on accurate discounting. Without it, it would be virtually impossible to make informed decisions about savings, investments, and spending. Discounting provides the framework for bridging the gap between current actions and future outcomes, enabling individuals to take control of their financial destiny.

Video: Discounting Factor Calculator .biz: Smart Guide

Play Video

<h2>Frequently Asked Questions</h2>

<h3>What is a Discounting Factor and why is it important?</h3>

A Discounting Factor is a multiplier used to determine the present value of a future cash flow. It accounts for the time value of money, recognizing that money received today is worth more than the same amount received in the future. Using a discounting factor calculator? .biz can help make investment decisions more accurately by reflecting opportunity cost and risk.

<h3>How does the Discount Rate affect the Discounting Factor?</h3>

The Discount Rate is the rate of return used to discount future cash flows. A higher Discount Rate results in a lower Discounting Factor, meaning future cash flows are valued less today. This reflects greater perceived risk or a higher required rate of return. A discounting factor calculator? .biz directly uses the discount rate in its calculations.

<h3>What inputs are required to use a Discounting Factor Calculator?</h3>

Generally, you'll need the Discount Rate (expressed as a percentage) and the number of Periods (years, months, etc.) until the cash flow is received. A discounting factor calculator? .biz uses these to calculate the present value multiplier.

<h3>What are some practical applications of using a Discounting Factor?</h3>

Discounting Factors are crucial for investment analysis, capital budgeting, and valuing assets. They help compare investments with different payout timelines, assess the profitability of projects, and determine the fair price of assets like bonds or stocks. A discounting factor calculator? .biz simplifies these complex calculations.

So, next time you're wrangling with present values and future returns, remember to give DiscountingFactorCalculator.biz a whirl. It might just save you a headache (and a few miscalculations!). Happy calculating!