Circumference of a Cylinder: Easy Calculation Guide

The circumference of a cylinder is a fundamental concept in geometry, particularly relevant in fields such as mechanical engineering where cylindrical shapes are common. Understanding this measurement often involves utilizing tools like calipers, which provide precise diameter readings necessary for accurate calculations. The relationship between the radius of a cylinder and its circumference is defined by mathematical constants such as pi (π), approximately 3.14159. Practical applications of calculating the circumference of a cylinder can be seen in manufacturing processes, where organizations such as the American Society of Mechanical Engineers (ASME) set standards for dimensional accuracy and precision.

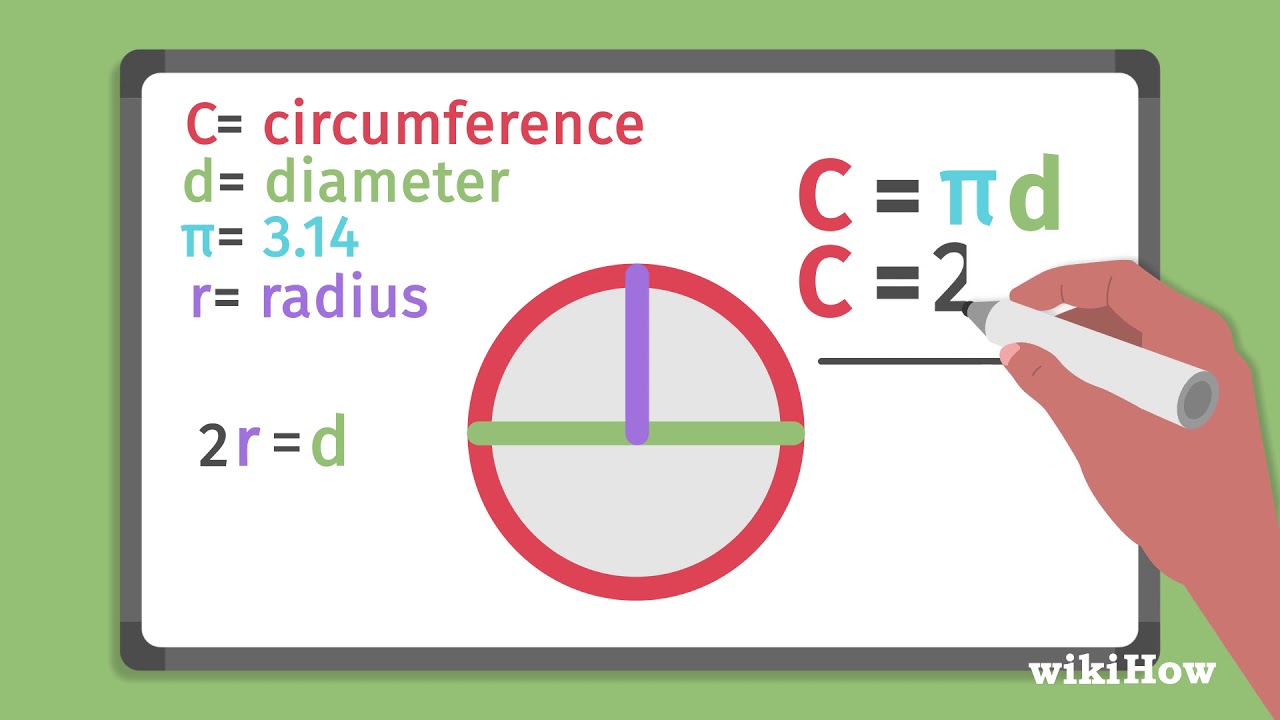
Image taken from the YouTube channel wikiHow , from the video titled How to Calculate the Circumference of a Circle .

Unveiling the Circumference of a Cylinder: A Foundational Concept

The concept of circumference, representing the distance around a circle, is a cornerstone of geometry and a crucial element in understanding the properties of cylindrical shapes. This introduction will explore the meaning of circumference, focusing specifically on its application to cylinders. We will establish its significance in various mathematical and real-world contexts.

Defining Circumference

At its core, circumference is the measurement of the total distance around the edge of a circle. Imagine walking along the very edge of a perfectly round shape; the total distance you cover is the circumference.

This measurement is fundamental, influencing countless calculations and designs. It serves as the basis for understanding areas, volumes, and the relationships between different geometric figures.

Understanding Cylinders and Their Circular Bases

A cylinder is a three-dimensional geometric shape characterized by two parallel circular bases connected by a curved surface. The circular bases are integral to defining a cylinder.

Think of a can of soup or a cardboard tube – these are everyday examples of cylinders. The circumference of either circular base is critical for determining the cylinder's overall dimensions and properties.

The Significance of Circumference: Calculations and Real-World Applications

Understanding circumference is not merely an academic exercise; it has profound practical implications. The ability to accurately calculate the circumference of a cylinder's base allows us to determine how much material is required to wrap around it or to calculate its surface area and volume.

Circumference plays a vital role in numerous fields, from engineering and manufacturing to construction and even art. Consider the precise calculations needed to design a cylindrical pipe, manufacture a can, or construct a cylindrical building component.

In all of these scenarios, an understanding of circumference is indispensable. We are setting the stage for a deeper exploration of its mathematical foundation and real-world significance. From the design of everyday objects to complex engineering projects, the principles of circumference provide a fundamental basis for accurate calculation and design.

Essential Mathematical Foundations: Diameter, Radius, and Pi

To accurately determine the circumference of a cylinder, a solid grasp of several fundamental mathematical concepts is indispensable. These include understanding the diameter and radius of a circle, as well as the significance of the mathematical constant Pi (π). Mastering these concepts provides the essential foundation for calculating circumference with precision.

Defining Diameter and Radius

The diameter of a circle, typically denoted as 'd', is defined as the distance across the circle passing through its center. In essence, it is the longest possible straight line segment that can be drawn from one point on the circle to another. The diameter effectively bisects the circle into two equal halves.

The radius, represented by 'r', is the distance from the center of the circle to any point on its circumference. It is precisely half the length of the diameter. The radius is also critically important for determining the area of a circle, and subsequently the surface area and volume of a cylinder.

The Relationship Between Diameter and Radius

The relationship between diameter and radius is straightforward and crucial. The diameter is always twice the length of the radius. This can be expressed mathematically as:

d = 2r

Conversely, the radius is half the length of the diameter:

r = d/2

Understanding this relationship is essential for seamlessly transitioning between diameter and radius measurements when calculating circumference and other circular properties.

Understanding Pi (π): A Fundamental Constant

Pi (π) is a mathematical constant representing the ratio of a circle's circumference to its diameter. It is an irrational number, meaning its decimal representation neither terminates nor repeats. Pi is approximately equal to 3.14159, although its decimal representation extends infinitely.

Pi is a fundamental constant found ubiquitously in mathematics, physics, and engineering. Its presence allows us to relate the linear dimension of a circle (diameter or radius) to its circumference.

The Significance of Pi

The significance of Pi lies in its ability to provide a consistent relationship between a circle's diameter and its circumference, regardless of the circle's size. This consistency makes it invaluable for a wide range of calculations related to circles and spheres.

Without Pi, accurately calculating circumference, area, surface area, and volume would be impossible. Understanding Pi is, therefore, essential.

Formulas for Calculating Circumference

With a clear understanding of diameter, radius, and Pi, calculating the circumference of a circle (and, by extension, the circular base of a cylinder) becomes straightforward. The two primary formulas for calculating circumference are:

1. Using the diameter:

C = πd

Where 'C' represents the circumference and 'd' represents the diameter.

2. Using the radius:

C = 2πr

Where 'C' represents the circumference and 'r' represents the radius.

Both formulas will yield the same result; the choice of which to use depends on whether you know the diameter or the radius of the circle. Mastery of these formulas, and the concepts they represent, is essential for effectively working with circles and cylinders in various mathematical and practical applications.

Expanding on Circular Relationships: Area, Surface Area, and Volume

Having established a solid understanding of circumference, diameter, radius, and Pi, it is logical to extend these concepts to explore related properties of circles and, more specifically, cylinders. These properties include the area of a circle, the surface area of a cylinder, and the volume of a cylinder. Each builds upon the fundamental understanding of circular dimensions and reveals further insights into the characteristics of these shapes.

Area of a Circle: The Space Within

The area of a circle represents the two-dimensional space enclosed within its circumference. It quantifies the total surface contained by the circle's boundary. The formula for calculating the area (A) of a circle is expressed as:

A = πr²

Where 'π' (Pi) is the mathematical constant (approximately 3.14159) and 'r' is the radius of the circle.

This formula highlights the importance of the radius. A small change in the radius significantly impacts the area, due to the squared relationship. Understanding area is crucial for numerous applications, from calculating the cross-sectional area of pipes to determining the material needed for circular designs.

Surface Area of a Cylinder: Wrapping the Shape

The surface area of a cylinder is the total area covering its exterior. This includes the area of the two circular bases (top and bottom) and the lateral surface area (the curved side). Accurately calculating the surface area is vital in contexts ranging from manufacturing to heat transfer analysis.

The formula for the surface area (SA) of a cylinder is given by:

SA = 2πrh + 2πr²

Where 'r' is the radius of the circular base, 'h' is the height of the cylinder, and 'π' is Pi.

This formula can be broken down into two components: 2πrh, representing the lateral surface area (the circumference of the base multiplied by the height), and 2πr², representing the combined area of the two circular bases.

The Role of Circumference

Notice that the term 2πr appears in the surface area formula. This component directly reflects the circumference of the circular base. Therefore, a thorough understanding of circumference is essential for accurately determining the surface area of a cylinder. Without it, calculating the lateral surface area becomes significantly more challenging.

Volume of a Cylinder: Measuring Capacity

The volume of a cylinder refers to the amount of three-dimensional space it occupies. It indicates the cylinder's capacity, determining how much it can hold. Volume calculations are crucial in various fields, including fluid mechanics, storage tank design, and material estimation.

The formula for the volume (V) of a cylinder is:

V = πr²h

Where 'r' is the radius of the circular base, 'h' is the height of the cylinder, and 'π' is Pi.

This formula reveals that the volume is the product of the area of the circular base (πr²) and the cylinder's height (h). A clear understanding of the relationship between radius and height is paramount.

Radius and Height Relationship

The formula V = πr²h emphasizes how the volume changes proportionally with both the radius and the height. A larger radius results in a greater cross-sectional area, leading to a higher volume. Similarly, a greater height directly increases the volume. Understanding this interplay is crucial for optimizing cylindrical designs and accurately predicting their capacity.

Measuring Circumference: Units and Tools

Having established the theoretical foundation for understanding and calculating circumference, we now turn to the practical aspects of measurement. Accurate measurement is crucial for real-world applications, and the choice of tools and units plays a significant role in achieving precision. This section will guide you through the standard units of measurement and the essential tools needed to accurately measure circles and cylinders, and subsequently calculate their circumference.

Standard Units of Measurement

The circumference, being a linear measurement, is expressed using units of length. The selection of an appropriate unit depends on the scale of the object being measured and the desired level of precision. Common units include:

• Inches (in): Often used for smaller objects and in contexts where the imperial system is prevalent.

• Centimeters (cm): A standard unit in the metric system, suitable for moderate-sized objects and everyday measurements.

• Meters (m): Used for larger objects and distances, providing a more convenient scale for architectural or construction applications.

• Feet (ft): Another unit from the imperial system, commonly used in construction and for measuring larger dimensions.

It's crucial to maintain consistency within a calculation. Converting all measurements to a single unit before applying the circumference formulas (C = πd or C = 2πr) is vital for avoiding errors and ensuring accurate results.

Tools for Direct Measurement

Direct measurement of circumference involves physically measuring the distance around a circular object. Several tools are available for this purpose, each offering its own advantages and limitations:

• Rulers and Measuring Tapes: These tools are straightforward and widely accessible. However, directly measuring the circumference of a curved object with a ruler can be challenging and prone to inaccuracies. Flexible measuring tapes offer better conformity to curved surfaces, yielding more accurate results.

• Compasses: While not directly used for measuring circumference, compasses are invaluable for constructing circles of a specific radius. Once the radius is determined, the circumference can be easily calculated using the formula C = 2πr.

• Calipers: External calipers can be used to measure the diameter of the circle. From there, the circumference can be calculated using the formula C = πd.

The Role of Calculators: Physical and Online

Calculators are indispensable tools for efficiently and accurately computing circumference values. Both physical and online calculators offer features that simplify these calculations:

• Physical Calculators: Scientific calculators with a dedicated Pi (π) function are highly recommended. These calculators store Pi to a greater degree of accuracy, reducing rounding errors in the final result. Using the Pi function is almost always better than manually entering 3.14 or 3.14159.

• Online Circumference Calculators: Numerous websites provide dedicated circumference calculators. These tools typically require the user to input either the radius or the diameter, and they instantly compute the circumference. Online calculators offer convenience and accessibility, particularly for quick calculations or when a physical calculator is not readily available.

Choosing the Right Tool

The choice of measurement tool depends on the desired accuracy and the context of the application. For rough estimates or quick checks, a ruler or measuring tape may suffice. However, for applications requiring high precision, a scientific calculator with a Pi function and direct diameter/radius measurement using appropriate calipers is essential. In situations where direct physical measurement is impractical, online calculators offer a convenient and readily accessible alternative.

Digital Resources: Online Calculators, Educational Sites, and Spreadsheets

In the digital age, numerous resources are available to streamline circumference calculations and enhance understanding. From specialized online calculators to comprehensive educational platforms and versatile spreadsheet software, these tools offer diverse approaches to mastering this fundamental concept. This section explores these digital avenues, providing a guide to leveraging technology for accurate calculations and in-depth learning.

The Convenience of Online Circumference Calculators

Online circumference calculators offer immediate solutions for determining circumference when the radius or diameter is known. These tools are readily accessible via any web browser and often feature user-friendly interfaces.

The primary advantage lies in their speed and simplicity, allowing users to bypass manual calculations and obtain results instantly. Many calculators also provide options for specifying units of measurement (e.g., inches, centimeters, meters), further enhancing their practicality.

However, it's important to verify the calculator's accuracy and understand the underlying formulas. Relying solely on online calculators without grasping the core principles can hinder genuine comprehension.

Exploring Educational Websites for In-Depth Learning

Educational websites provide a wealth of information and resources for learning about circumference and related geometrical concepts. Platforms like Khan Academy offer structured lessons, video tutorials, and practice exercises that cater to various learning styles.

Math is Fun provides clear, concise explanations and interactive tools that make learning engaging. These websites offer comprehensive coverage, from basic definitions to advanced applications, making them invaluable resources for students and educators alike.

These resources extend beyond formulas. They often incorporate real-world examples and problem-solving techniques to foster a deeper understanding of circumference's significance.

The Role of Traditional and Digital Textbooks

Textbooks, in both physical and digital formats, remain essential resources for studying circumference and geometry. Traditional textbooks offer comprehensive explanations, worked examples, and practice problems, providing a structured learning path.

Digital textbooks enhance this experience with interactive elements, multimedia content, and search functionality. Publishers like Pearson and McGraw-Hill offer a wide range of mathematics textbooks that cover circumference in detail, along with supplementary online resources.

Textbooks provide a foundational understanding and serve as reliable references for students and professionals alike.

Leveraging Spreadsheet Software: Excel and Google Sheets

Spreadsheet software, such as Microsoft Excel and Google Sheets, can be powerful tools for calculating and analyzing circumference. These programs allow users to input values for the radius or diameter and apply formulas to automatically calculate the circumference.

For example, in Excel, you can enter the formula “=2PI()A1” to calculate the circumference when the radius is in cell A1. Spreadsheets also enable you to create tables and graphs, facilitating the visualization of data and the exploration of relationships between different variables.

Furthermore, the collaborative features of Google Sheets allow multiple users to work on the same spreadsheet simultaneously, making it ideal for group projects and collaborative learning.

Spreadsheet software enhances problem-solving capabilities and fosters a deeper understanding of mathematical concepts.

Real-World Applications: Engineering, Manufacturing, and More

The calculation of circumference, seemingly a basic geometrical concept, resonates deeply across numerous professional fields. Its applications extend far beyond the classroom, underpinning critical calculations and designs in engineering, manufacturing, construction, physics, architecture, and beyond. Understanding these applications demonstrates the enduring relevance of this fundamental mathematical principle.

Engineering Applications: Precision and Design

In the diverse realm of engineering, circumference plays a pivotal role in various disciplines. Mechanical engineers rely on it to calculate the dimensions of rotating components, such as gears, shafts, and turbines. Civil engineers employ it in designing circular structures like tunnels, bridges, and pipelines.

Electrical engineers utilize it in determining the length of wire needed to coil transformers and motors. The precise calculation of circumference ensures optimal performance and structural integrity in these critical systems.

Manufacturing of Cylindrical Products: Accuracy and Efficiency

The manufacturing sector heavily depends on accurate circumference calculations for producing a wide array of cylindrical products. From pipes and tubes to containers and rollers, the dimensions of these items are crucial for their functionality and compatibility.

Manufacturers use circumference to determine the amount of material needed for production, minimize waste, and ensure consistent quality. Precise circumference calculations streamline production processes and reduce the risk of defects.

Construction Projects: Structural Integrity and Safety

In construction, circumference is essential for creating stable and aesthetically pleasing circular structures. Architects and engineers use it to design domes, arches, and cylindrical columns.

Circumference calculations are also vital for ensuring the proper fit and alignment of pipes, conduits, and other cylindrical components in buildings and infrastructure. Accurate calculations contribute to the structural integrity and safety of construction projects.

Mathematics Education: Building Foundations and Beyond

Understanding circumference is a cornerstone of mathematics education. It forms a foundation for more advanced concepts in geometry, trigonometry, and calculus.

By mastering the concept of circumference, students develop critical problem-solving skills and gain a deeper appreciation for the power of mathematical principles. Circumference serves as a gateway to more complex mathematical concepts.

Physics: Circular Motion and Beyond

In physics, circumference is fundamental in calculations involving circular motion. It is used to determine the distance traveled by an object moving along a circular path, as well as its speed and acceleration.

Applications include calculating the orbital paths of planets, the rotation of wheels, and the movement of particles in a cyclotron. Circumference provides the framework for understanding motion in circular paths.

Architecture: Design and Aesthetics

Architects utilize circumference in the design of cylindrical architectural elements such as columns, towers, and domes. The accurate calculation of circumference ensures that these elements are both aesthetically pleasing and structurally sound.

Circumference also plays a role in the design of curved walls and other rounded features that add visual interest and architectural flair to buildings. Circumference connects mathematical precision to aesthetic architectural design.

Professionals and Learners: Who Uses Circumference?

The understanding and application of circumference extend far beyond the realm of theoretical mathematics. Numerous professionals and learners regularly employ this fundamental concept in their daily work and studies. Let's examine some key groups and how they utilize circumference calculations.

Mathematics Teachers and Educators: Guiding the Next Generation

Mathematics teachers and educators form the bedrock of circumference knowledge dissemination. They introduce the concept to students, guiding them through the formulas and practical applications.

Educators design lessons that demonstrate the real-world relevance of circumference, using examples from everyday life and various professions. They foster a deeper understanding of mathematical principles and promote critical thinking skills.

Teachers also assess student comprehension and provide feedback, ensuring that learners grasp the concept of circumference before moving on to more advanced topics. They are critical in laying the foundation for future STEM professionals.

Engineers: Designing and Innovating with Precision

Engineers across various disciplines rely heavily on circumference calculations in their design and analysis processes. Mechanical engineers, for example, use circumference to determine the dimensions of rotating parts, such as gears, shafts, and wheels.

Civil engineers apply it to design circular structures like tunnels, pipes, and support columns. Electrical engineers calculate wire lengths for coils in transformers and motors, ensuring optimal performance.

Mechanical Engineering

Mechanical engineers need to be especially careful with diameter calculations. The relationship between the diameter and circumference is crucial for calculating the efficiency, for example, of a rotor or generator. Mechanical engineers are also concerned with the stress of a circle, especially one that has different pressures on either side.

Civil Engineering

In civil engineering, circumference calculations are crucial for various projects. Estimating the material needed for a pipe is often an important first step in designing a piping system. Calculating the load for a pipe requires complex equations that depend on circumference to estimate the load the circular pipe can handle.

Electrical Engineering

Electrical engineers require circumference knowledge to accurately wind coils for inductors and transformers. Precision here is extremely important. Poorly wound coils impact overall performance of a design and often cause the entire design to fail.

The accurate calculation of circumference ensures that these components meet the required specifications and function correctly within complex systems. Precision is paramount in engineering applications, and circumference plays a vital role in achieving it.

Students: Building a Foundation for Future Success

Students encounter circumference early in their mathematics education, typically in geometry courses. Learning about circumference provides a foundation for understanding more advanced concepts, such as area, volume, and trigonometry.

By solving problems involving circumference, students develop their problem-solving skills and learn to apply mathematical principles to real-world scenarios. This understanding is crucial for success in future STEM-related fields.

Furthermore, understanding circumference helps students appreciate the interconnectedness of mathematical concepts and their relevance to various disciplines. The knowledge of circumference is therefore more than just remembering a formula.

Mathematical Connections: Circumference within Geometry

Understanding circumference isn't merely about memorizing formulas; it's about grasping its place within the larger, elegant framework of geometry. Circumference is a foundational concept, acting as a crucial link to other geometric principles and mathematical constants.

By exploring these connections, we gain a richer, more nuanced appreciation for the power and interconnectedness of mathematics.

Circumference: A Geometric Cornerstone

Circumference is intrinsically linked to the circle, one of the most fundamental shapes in geometry. A circle's circumference defines its boundary, a single line whose length is precisely what we calculate using the familiar formulas.

It's not an isolated measurement, but rather a key property that defines a circle's size and, consequently, its relationship to other geometric figures.

Consider, for example, the relationship between a circle and a square. One can inscribe a circle within a square, or circumscribe a circle around a square.

In both cases, the circumference plays a critical role in understanding the geometric relationship and calculating dimensions.

Interplay with Area and Volume

The concept of circumference naturally extends to the calculation of other crucial properties of circles and cylinders. The area of a circle, given by πr², is directly dependent on the radius, which is, in turn, related to the circumference.

Similarly, when calculating the surface area or volume of a cylinder, the circumference of the circular base becomes a vital component.

The surface area involves circumference and area calculations, while volume involves area and the cylinder's height.

These relationships highlight the interdependence of geometric concepts and how understanding circumference facilitates a deeper comprehension of more complex shapes.

Pi (π) and Other Mathematical Constants

While Pi (π) is most directly linked to circumference, it is but one of many fundamental mathematical constants. Understanding constants is crucial to grasp many mathematical concepts.

Pi is transcendental, which means it is not the root of any non-zero polynomial equation with integer coefficients. This quality makes Pi infinitely non-repeating.

A Brief Look at Euler's Number (e)

Euler's number, denoted as e, is another prominent mathematical constant, approximately equal to 2.71828. While not directly involved in circumference calculations, e demonstrates the broader landscape of mathematical constants that govern various phenomena.

e appears in calculus, exponential growth, and complex number calculations. It is indispensable in understanding the natural world through mathematical modeling.

Acknowledging the existence and importance of constants like e broadens our appreciation for the underlying mathematical structures that govern diverse aspects of the world around us.

Resources and Support: Mathematics Organizations

For individuals seeking to deepen their understanding of mathematics, professional organizations offer a wealth of resources, support, and community. These organizations play a crucial role in advancing mathematics education, promoting research, and fostering a greater appreciation for the field. They are a critical link between theoretical knowledge and practical application, providing avenues for professional development and networking.

The National Council of Teachers of Mathematics (NCTM)

The National Council of Teachers of Mathematics (NCTM) stands as a leading voice in mathematics education. Its primary focus is to improve the teaching and learning of mathematics from pre-K through 12th grade. This organization is a cornerstone for educators looking to enhance their skills and knowledge.

NCTM's Role in Education

NCTM provides a range of resources, including professional development opportunities, publications, and research-based materials. Its conferences and workshops are invaluable for teachers seeking to stay current with best practices and emerging trends in mathematics education.

The organization's publications, such as Teaching Children Mathematics, Mathematics Teaching in the Middle School, and Mathematics Teacher, offer insightful articles, lesson ideas, and perspectives on key issues in mathematics education. These publications provide a platform for educators to share their experiences and learn from others in the field.

By setting standards and providing resources, NCTM significantly shapes how mathematics is taught and learned in schools across the nation.

NCTM Standards

NCTM has been instrumental in developing influential standards for mathematics education. These standards provide a framework for curriculum development and assessment, ensuring that students acquire the essential mathematical knowledge and skills needed for success in college and careers.

The Principles and Standards for School Mathematics, published in 2000, outlined a comprehensive set of recommendations for mathematics education. These recommendations have served as a guide for educators and policymakers in shaping mathematics curricula and instruction.

NCTM continues to update and refine its standards to reflect the evolving needs of students and society. Their work remains a critical component of the mathematics education landscape.

Other Notable Mathematics Organizations

Beyond NCTM, numerous other organizations contribute to the advancement of mathematics. These organizations cater to a variety of interests and professional levels, offering diverse opportunities for engagement and growth.

The American Mathematical Society (AMS)

The American Mathematical Society (AMS) is dedicated to advancing mathematical research and scholarship. It serves as a vital resource for mathematicians at all stages of their careers. The AMS publishes journals, organizes conferences, and supports various programs that promote mathematical discovery and dissemination.

The Mathematical Association of America (MAA)

The Mathematical Association of America (MAA) focuses on mathematics at the undergraduate level. It promotes excellence in teaching and learning. The MAA provides resources for faculty, organizes competitions for students, and publishes journals and books on various mathematical topics.

Society for Industrial and Applied Mathematics (SIAM)

The Society for Industrial and Applied Mathematics (SIAM) connects mathematics with real-world applications in science, engineering, and industry. It supports research in applied mathematics and provides opportunities for collaboration between mathematicians and professionals in other fields. SIAM publishes journals, organizes conferences, and offers educational resources for students and professionals.

Leveraging Organizational Resources

Mathematics organizations provide opportunities to present research, network with peers, and engage in professional development. By actively participating in these communities, individuals can stay abreast of the latest developments in the field, enhance their skills, and contribute to the advancement of mathematical knowledge.

Whether you are a student, a teacher, or a researcher, exploring the resources offered by mathematics organizations can significantly enhance your mathematical journey.

Video: Circumference of a Cylinder: Easy Calculation Guide

Play Video

So, there you have it! Calculating the circumference of a cylinder doesn't have to be a headache. With these simple steps and a little practice, you'll be finding the circumference of a cylinder like a pro in no time. Happy calculating!